Тождество Якоби — Билинейная операция на линейном пространстве называется удовлетворяющей тождеству Якоби, если: Названо в честь Карла Густава Якоби. Понятие тождества Якоби обычно связано с алгебрами Ли. Содержание … Википедия
ПУАССОНА СКОБКИ — важное понятие аналитич. механики, введённое С. Пуассоном (S. Poisson) в 1809 и получившее дальнейшее развитие в гамильтоновой механике (см. Гамильтонов формализм). П. с. могут быть обобщены на случай квантовой механики, а также классич. и… … Физическая энциклопедия
ПУАССОНА СКОБКИ — дифференциальное выражение , (1) зависящее от двух функций u(q, р). и v(q, р) 2п переменных q=(q1 ,. . ., qn), p=(p1, . . ., р n). Введены С. Пуассоном [1]. П. с. частный: случай Якоби скобок. П. с. есть билинейная форма от функций и, v, причем и … Математическая энциклопедия
ПОЛНАЯ СИСТЕМА — замкнутая система (дифференциальных уравнений), система дифференциальных уравнений с частными производными 1 го порядка (1) со следующим свойством: для любого набора чисел ( х, и, р), удовлетворяющего уравнениям (1), справедливы равенства где Fij … Математическая энциклопедия
ИНВОЛЮЦИОННАЯ СИСТЕМА — система дифференциальных уравнений c частными производными 1 го порядка где х=( х 1, ..., х n), и=и{х 1, . .., х п),р=( р 1, . .., р n)=( )., для к рой все Якоби скобки равны нулю тождественно по ( х, и, р). Равенства (2) наз. условиями… … Математическая энциклопедия
ИНТЕГРАЛЫ В ИНВОЛЮЦИИ — решения дифференциальных уравнений, Якоби скобки к рых равны нулю. Функция G(x, и, р)2n+1 переменных х=(x1, ..., х п), и, р=( р 1, ..., р п) еcть первый интеграл уравнения с частными производными первого порядка если она постоянна вдоль каждой… … Математическая энциклопедия
Вектор Лапласа — Рунге — Ленца — В этой статье векторы выделены жирным шрифтом, а их абсолютные величины курсивом, например, . В классической механике вектором Лапласа Рунге Ленца называется вектор, в основном используемый для описания формы и ориентации орбиты, по… … Википедия
Вектор эксцентриситета — В этой статье векторы и их абсолютные величины выделены жирным шрифтом и курсивом, например, . В классической механике вектором Лапласа Рунге Ленца называется вектор, в основном используемый для описания формы и ориентации орбиты, по которой… … Википедия
Вектор Лапласа-Рунге-Ленца — В этой статье векторы и их абсолютные величины выделены жирным шрифтом и курсивом, например, . В классической механике вектором Лапласа Рунге Ленца называется вектор, в основном используемый для описания формы и ориентации орбиты, по которой… … Википедия
Вектор Лапласа — В этой статье векторы выделены жирным шрифтом, а их абсолютные величины курсивом, например, . В классической механике вектором Лапласа Рунге Ленца называется вектор, в основном используемый для описания формы и ориентации орбиты, по… … Википедия
где принято символическое обозначение 
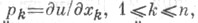то (2) приобретает смысл полной производной по х k. Если функции Fи Gне зависят от и, то их Я. с. (1) переходит в Пуассона скобку. 