- ПОЛНАЯ СИСТЕМА
, замкнутая система (дифференциальных уравнений), - система дифференциальных уравнений с частными производными 1-го порядка
(1)
со следующим свойством: для любого набора чисел ( х, и, р), удовлетворяющего уравнениям (1), справедливы равенства
где Fij=[Fi, Fj] - Якоби скобки.
Для линейных однородных систем условие полноты (формулируется несколько иначе. Скобка Якоби в этом случае линейна по переменным p=(p1, . . ., р n), и если система записана в виде
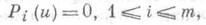
где Pi - линейные дифференциальные операторы 1-го порядка, то этой скобке отвечает коммутатор [Р i, Р j]=PiPj-PjPi. Полнота системы заключается в представимости всех коммутаторов [ Р i, Р j]в виде линейных комбинаций от Р k, с коэффициентами, зависящими только от х=( х 1, . . ., х n).
Если и=и (х) - совместное решение двух уравнений
то иявляется решением и уравнения
(2),
Произвольную систему вида (1) обычно пытаются расширить до полной добавлением к ней новых независимых уравнений, полученных из старых с помощью операции образования скобок Якоби. При этом расширении в соответствии с (2) ни одно из решений переходной системы не должно теряться, если она вообще разрешима.
Свойство системы быть полной инвариантно относительно тех неособых преобразований переменных ( х, и, р, F), для к-рых сохраняется смысл дифференциальных уравнений. К таким преобразованиям относится, напр., замена независимых переменных х=g(y), y=(y1,...yn),a также преобразование следующего типа. Пусть
- такое гладкое отображение, что
есть диффеоморфизм
. Тогда рассматриваемое преобразование заключается в переходе от системы (1) к системе
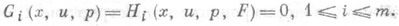
Лит.:[1] Камке Э., Справочник по дифференциальным уравнениям в частных производных первого порядка, пер. с нем., М., 1966; [2] Гюнтер Н. М., Интегрирование уравнений первого порядка в частных производных, Л.- М., 1934; [3] Caratheodory С., Variationsrechnung und partielle Differentialgleichungen erster Ordnung, 2 Aufl., Bd 1, Lpz., 1956; [4] Gоursat E., Lemons sur 1'integration des equations aux derivdes partielles du premier ordre, P., 1891. А. П. Солдатов.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
