- ИНВОЛЮЦИОННАЯ СИСТЕМА
- система дифференциальных уравнений c частными производными 1-го порядка
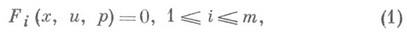
где х=( х 1, ..., х n), и=и{х 1, . .., х п),р=( р 1, . .., р n)=(
)., для к-рой все Якоби скобки равны нулю
тождественно по ( х, и, р). Равенства (2) наз. условиями разрешимости.
Для квазилинейных систем это определение несколько видоизменяется. Пусть все функции
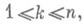не зависят от р= (р 1, ..., р n).
Тогда этим свойством обладают и функции
В классе квазилинейных уравнений условие инволюционности системы определяется равенствами
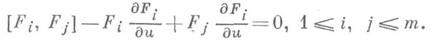
Когда Fi не зависят от и, это определение совпадает с предыдущим. Иногда последнее определение инволюционности распространяют на все системы вида (1). Если система (1) линейна, однородна и записана в виде
где Pi- линейные дифференциальные операторы 1-го порядка, то ее инволюционность можно определить как условие коммутируемости PiPj=PjPi для всех
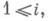
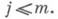
Всякая И. с. является полной системой. Обратно, если (1) полная система и имеет нормальную форму, т. е.
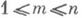и Fi(x, и, p) = pi- fi(x, и, р т+1,..., р n),
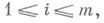то она инволюционна. Это позволяет привести полную систему к И. с, если 
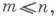и ее можно разрешить неособым преобразованием относительно нек-рых тпеременных p=(p1, ..., р п).Если система (1) не зависит от и, т=п, определитель
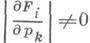и pi=pi(x)разрешены из уравнений Fi(x,р)=
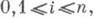то инволюционность этой системы означает, что выражение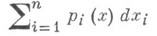
является полным дифференциалом. На этом основано применение метода Якоби [2] решения И. с, не зависящих от ии состоящих из in функционально независимых уравнений, т<п. В соответствии с этим методом исходную систему расширяют до И. с. из пуравнений с вышеуказанными свойствами. Расширение идет в несколько этапов, каждая последующая система получается из предыдущей добавлением ее независимых первых интегралов в инволюции. Этот метод допускает применение и для системы уравнений, зависящей от и(см. [3]).
Лит.:[1] Caratheodory С, Variationsrechnung und partielle Differentialgleichungen erster Ordnung, 2 Aufl., Lpz., 1956; [2] Jасоbi C, "J. reine und angew. Math.", 1862, Bd 60, S. 1-181; [3] Soursat E., Lecons sur l'integration des equations aux derive'es partielles du premier ordre, P., 1891; [4] Гюнтер Н. М., Интегрирование уравнений первого порядка в частных производных, Л.- М., 1934; [5] Камке Э., Справочник по дифференциальным уравнениям в частных производных первого порядка, пер. с нем., М., 1966.
А. П. Солдатов.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
