ЭНДОМОРФИЗМОВ КОЛЬЦО

ассоциативное кольцо End А=Ноm(A, А), состоящее из всех морфизмов . в себя, где А - объект нек-рой аддитивной категории С. Умножение в End Асовпадает с композицией морфизмов, а сложение - со сложением морфизмов, определенным аксиомами аддитивной категории. Тождественный морфизм 1_A является единицей кольца End A. Элемент из End Аобратим тогда и только тогда, когда - автоморфизм объекта А. Если Aи В- нек-рые объекты категории С, то группа Ноm ( А, В )обладает естественной структурой правого модуля над кольцом End Аи левого модуля над кольцом End В. Пусть - ковариантный (соответственно контравариантный) аддитивный функтор из аддитивной категории Св аддитивную категорию С'. Тогда для любого объекта Аиз С функтор Тиндуцирует естественный гомоморфизм (соответственно естественный антигомоморфизм) End
Пусть С - категория модулей над кольцом R. Для R-модуля Акольцо End Асостоит из всех эндоморфизмов абелевой группы А, перестановочных с умножением на элементы из R. Сумма эндоморфизмов определяется формулой
Если R - коммутативно, то кольцо End Аобладает естественной структурой R-алгобры. Многие свойства модуля Амогут быть охарактеризованы в терминах кольца End А. Напр., модуль Анеприводим тогда и только тогда, когда End Аявляется телом.
Произвольный гомоморфизм p ассоциативного кольца Кв End Аназ. представлением кольца . (эндоморфизмами объекта А). Если К - кольцо с единицей, то накладывается дополнительное условие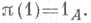 Любое ассоциативное кольцо Кобладает точным представлением в Э. к. нек-рой абелевой группы А. Причем, если К - кольцо с единицей, то в качестве Аможно взять аддитивную группу кольца К, на к-рую элементы из K действуют умножением слева. Если же К - кольцо без единицы и K'- кольцо, полученное из Квнешним присоединением единицы к К, то в качестве Аможно взять аддитивную группу кольца K'.
В случае абелева многообразия Xнаряду с кольцом End A , являющимся конечно порожденным -модулем, рассматривают алгебру эндоморфизмов (алгебру комплексных умножений)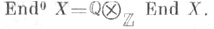

Лит.:[1] Фейс К., Алгебра: кольца, модули и категории, т. 1-2, пер. с англ., М., 1977-79; [2] Мaмфорд Д., Абелевы многообразия, пер. с англ., М., 1971; [3] Итоги науки и техники. Алгебра. Топология. Геометрия, т. 21, М., 1983, с. 183-254.
Л. В. Кузьмин.