- РИККАРТОВО КОЛЬЦО
левое, л е в о е РР-кольцо, - кольцо, в к-ром левый аннулятор любого элемента порождается идемпотентом (симметричным образом определяются п р а в ы е Р. к.). Р. к. характеризуются проективностью всех главных левых (правых) идеалов. Риккартовыми являются регулярные, бэровские и полунаследственные кольца. Левое Р. к. не обязано быть правым Р. к. Может не быть риккартовым и кольцо матриц над Р. к. Кольца эндоморфизмов всех свободных левых R-модулей суть Р. к. тогда и только тогда, когда Rнаследственно слева. Все эти кольца будут правыми Р. к. в том и только в том случае, когда R наследственно слева, совершенно слева и когерентно справа. Сами же кольца эндоморфизмов при этих условиях оказываются бэровскими (см. Регулярное кольцо). Коммутативное кольцо Rявляется Р. к. тогда и только тогда, когда его полное кольцо частных регулярно в смысле Неймана и для всякого максимального идеала
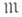 кольца Rкольцо частных
кольца Rкольцо частных  не имеет делителей нуля. Кольцо многочленов над коммутативным Р. к. является Р. к.
не имеет делителей нуля. Кольцо многочленов над коммутативным Р. к. является Р. к.
Кольцо с инволюцией * наз. р и к к а р т о в ы м *- к о л ь ц о м, если левый аннулятор любого элемента порождается проекцией, т. е. таким элементом е, что
 . Аналогичное свойство для правых аннуляторов при этом выполняется автоматически. Проекции риккартова *-кольца образуют решетку. Эта решетка полна в том и только в том случае, когда проекцией порождается аннулятор любого множества. Такие кольца наз. б э р о в с к и м и * - кольцами.
. Аналогичное свойство для правых аннуляторов при этом выполняется автоматически. Проекции риккартова *-кольца образуют решетку. Эта решетка полна в том и только в том случае, когда проекцией порождается аннулятор любого множества. Такие кольца наз. б э р о в с к и м и * - кольцами.
Термин "Р. к." введен в честь Ч. Риккарта, рассмотревшего соответствующее свойство в кольцах операторов (см. [1]).
Лит.:[1] R i с k а r t С. Е., "Ann. math.", 1946, v. 47, p. 528-50; [2] B e r b e r i a n S. K., B a e r *-rings, В- [а. о.], 1972; [3] К а р 1 a n s k у J., Rings of operators, N. Y.- Amst., 1968; [4] Итоги науки и техники. Алгебра. Топология. Геометрия, т. 15, М., 1981, с. 31 - 134. Л. А. Скорняков.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
