КВАЗИФРОБЕНИУСОВО КОЛЬЦО

QF-к ольцо,- артиново кольцо (слева и справа), удовлетворяющее аннуляторным условиям:

для каждого левого (правого) идеала L(Н)(см. Аннулятор). Артиново слева кольцо, удовлетворяющее лишь одному из аннуляторных условий, может не быть К. к. Интерес к К. к. обусловлен наличием двойственности: артиново слева кольцо Л является К. к. тогда и только тогда, когда отображение

определяет двойственность категорий левых и правых конечно порожденных Л-модулей. Конечномерная алгебра Анад полем Роказывается К. к. в том и только том случае, когда каждое неприводимое прямое слагаемое левого A-модуля Нот _Р( А _A, Р )изоморфно нек-рому минимальному левому идеалу алгебры А. А это равносильно самодуальности решеток левых и правых идеалов алгебры А.

К. к. были введены как обобщение фробениусовых алгебр, определяемых требованием эквивалентности правого и левого регулярных представлений. Первоначально свойство артинова слева и справа кольца R быть квазифробениусовым определялось следующим условием: если e₁, ... , е _п- полный список примитивных идемпотентов из Л (т. е.при и, каков бы ни был примитивный идемпотент е,для нек-рого i), J- радикал кольца Rи j : R->R/J- естественный гомоморфизм, то найдется такая перестановка p множества {1, ... , п}, что

где Soc М- цоколь модуля М. Квазифробениусовость кольца Rэквивалентна также каждому из следующих свойств: (1) Rнётерово слева, для каждого правого идеала H и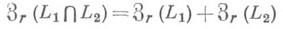

для любых левых идеалов L₁ и L₂; (2) Rудовлетворяет условию максимальности для левых (или правых) аннуляторных идеалов (в частности, если Rнётерово слева или справа) и самоинъективно слева или справа; (3) Rартиново справа и самоинъективно слева или справа; (4) каждый инъективный (проективный) левый R-модуль проективен (инъективен); (5) все плоские левые Л-модули инъективны; (6) Rсамоинъективно слева и справа и совершенно справа; (7) Rсамоинъективно слева и справа и каждый его правый идеал является аннулятором нек-рого конечного множества из R;(8) Rсовершенно справа и каждый конечно порожденный левый R-модуль вкладывается в проективный модуль; (9) Rкогерентно и совершенно справа и Ext_R (М, R) = 0 для всех конечно представимых левых R-модулей М;(10) Rудовлетворяет условию максимальности для левых аннуляторов и Ext_R(M, R) = 0 для всех конечно представимых левых Л-модулей М;(11) Л артиново слева и справа и для всякого конечно порожденного левого R-модуля Мдлины модулей Ми Hom_R(M, R) совпадают; (12) кольцо эндоморфизмов каждого свободного левого R-модуля самоинъективно слева; (13) конечно порожденные односторонние идеалы кольца эндоморфизмов любого проективного образующего (инъективного кообразующего) категории левых Л-модулей являются аннуляторами.

Инъективные модули над К. к. разлагаются в прямую сумму циклических. Для коммутативных колец справедливо и обратное. Если радикал Джекобсона J кольца Л трансфинитно нильпотентен (т. е. J^a=0 для нек-рого трансфинита а, где J¹=J, J^a=J^a-1J и для предельного а), то R - К. к. тогда и только тогда, когда R самоинъективно слева и все его односторонние идеалы аннуляторные. Левый модуль над К. к. Л точен в том и только в том случае, когда он является образующим категории левых R-модулей. Групповое кольцо RG является К. к. тогда и только тогда, когда группа Gконечна, а кольцо Л квазифробениусово.

Изучаются также нек-рые обобщения К. к.: левое QF-3-к ольцо Л определяется требованием существования точного левого R-модуля, вкладывающегося в качестве прямого слагаемого в любой точный левый R-модуль; левое QF-3'-к ольцо Л определяется требованием вложимости инъективной оболочки левого R-модуля R в прямое произведение нек-рого множества экземпляров модуля R. Левое псевдофробениусово кольцо (или левое PF- кольцо) определяется каждым из следующих свойств: а) R - инъективный кообразующий категории левых R-модулей; б) каждый точный левый Л-модуль является образующим категории левых Л-модулей; в) R - левое QF-3-кольцо и аннулятор любого отличного от Л правого идеала отличен от нуля.

Лит.:[1] Кэртис Ч., Райнер И., Теория представлений конечных групп и ассоциативных алгебр, пер. с англ., М., 1969; [2] Модули. [в.] 2, Новосиб., 1973, с. 42-48; [3] Ф е й с К., Алгебра: кольца, модули и категории, пер. с англ., т. 1-2, М., 1977-78.

Л. А. Скорняков.