ЭКСПОНЕНЦИАЛЬНОЕ ОТОБРАЖЕНИЕ
- ЭКСПОНЕНЦИАЛЬНОЕ ОТОБРАЖЕНИЕ
отображение касательного пространства многообразия Мв М, определяемое заданной на М связностью и являющееся далеко идущим обобщением обычной экспоненциальной функции, рассматриваемой как отображение прямой в себя.
1) Пусть М - многообразие класса 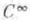 с аффинной связностью, р - нек-рая точка из М, М р - касательное пространство к многообразию Мв точке ри X - ненулевой вектор из
с аффинной связностью, р - нек-рая точка из М, М р - касательное пространство к многообразию Мв точке ри X - ненулевой вектор из 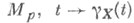 - геодезическая, проходящая через точку р в направлении вектора X. Существует такая открытая окрестность N0 точки 0 в М р и такая открытая окрестность N р точки рв М, что отображение
- геодезическая, проходящая через точку р в направлении вектора X. Существует такая открытая окрестность N0 точки 0 в М р и такая открытая окрестность N р точки рв М, что отображение  является диффеоморфизмом N0 на N р. Это отображение называется Э. о. в точке р и обозначается Ехр. Окрестность N0 наз. нормальной, если: 1) отображение Ехр диффеоморфно отображает N0 на N р,2) если
является диффеоморфизмом N0 на N р. Это отображение называется Э. о. в точке р и обозначается Ехр. Окрестность N0 наз. нормальной, если: 1) отображение Ехр диффеоморфно отображает N0 на N р,2) если  и
и 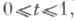 то
то 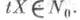 В этом случае N р - нормальная окрестность точки . в многообразии М. Каждая точка
В этом случае N р - нормальная окрестность точки . в многообразии М. Каждая точка 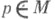 обладает выпуклой нормальной окрестностью N р точки р: любые две точки такой окрестности можно соединить в точности одним геодезич. отрезком, содержащимся в N р. Если М - полное риманово многообразие, то Ехр есть сюръективное отображение М р на М.
обладает выпуклой нормальной окрестностью N р точки р: любые две точки такой окрестности можно соединить в точности одним геодезич. отрезком, содержащимся в N р. Если М - полное риманово многообразие, то Ехр есть сюръективное отображение М р на М.
2)Пусть G- группа Ли с единицей еи g - соответствующая алгебра Ли, состоящая из касательных векторов к G в точке е. Для каждого вектора  существует единственный аналитич. омоморфизм
существует единственный аналитич. омоморфизм 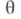 группы
группы 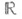 в Gтакой, что касательный вектор к
в Gтакой, что касательный вектор к 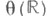 в точке есовпадает с X. Отображение
в точке есовпадает с X. Отображение  и наз. Э. о. алгебры gв группу G. Существует такая открытая окрестность N0 точки 0 в gи такая открытая окрестность N е точки ев G, что ехр является аналитич. диффеоморфизмом окрестности N0 на Ne. Пусть Х 1, ... , Х п - нек-рый базис алгебры g. Отображение
и наз. Э. о. алгебры gв группу G. Существует такая открытая окрестность N0 точки 0 в gи такая открытая окрестность N е точки ев G, что ехр является аналитич. диффеоморфизмом окрестности N0 на Ne. Пусть Х 1, ... , Х п - нек-рый базис алгебры g. Отображение 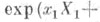
 есть система координат на Ne, эти координаты наз. каноническими.
есть система координат на Ne, эти координаты наз. каноническими.
К понятию Э. о. для группы Ли G можно подойти и с другой точки зрения. Существует взаимно однозначное соответствие между множеством всех аффинных связностей на G, инвариантных относительно группы левых сдвигов, и множеством билинейных функций 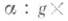
 Оказывается, что Э. о. ехр алгебры gв группу G совпадают с отображением Ехр касательного пространства gк многообразию . в точке ев это многообразие относительно лсвоинвариантной аффинной связности, отвечающей любой кососимметричной билинейной функции
Оказывается, что Э. о. ехр алгебры gв группу G совпадают с отображением Ехр касательного пространства gк многообразию . в точке ев это многообразие относительно лсвоинвариантной аффинной связности, отвечающей любой кососимметричной билинейной функции 
Лит.:[1] Xелгасoн С., Дифференциальная геометрия и симметрические пространства, пер. с англ., М., 1964.
А. С. Феденко.
Математическая энциклопедия. — М.: Советская энциклопедия.
И. М. Виноградов.
1977—1985.
Полезное
Смотреть что такое "ЭКСПОНЕНЦИАЛЬНОЕ ОТОБРАЖЕНИЕ" в других словарях:
Экспоненциальное отображение — далеко идущее обобщение экспоненциальной функции в римановой геометрии. Для риманова многообразия экспоненциальное отображение действует из касательного расслоения в само многообразие . Экспоненциальное отображение обычно обозначается , а его… … Википедия
ЛИ ГРУППА — группа G, обладающая такой структурой аналитического многообразия, что отображение прямого произведения в Gана литично. Другими словами, Ли г. это множество, наделенное согласованными структурами группы и аналитич. многообразия. Ли г. наз.… … Математическая энциклопедия
ГРУППА — множество, на к ром определена операция, наз. умножением и удовлетворяющая спец. условиям (групповым аксиомам): в Г. существует единичный элемент; для каждого элемента Г. существует обратный; операция умножения ассоциативна. Понятие Г. возникло… … Физическая энциклопедия
РИМАНОВА ГЕОМЕТРИЯ — теория риманова пространства. Р и м а н о в ы м п р о с т р а н с т в о м наз. n мерное связное дифференцируемое многообразие М п, на к ром задано дифференцируемое поле ковариантного, симметрического и положительно определенного тензора gранга 2 … Математическая энциклопедия
ГЕОДЕЗИЧЕСКАЯ ЛИНИЯ — геодезиче ская, геометрическое понятие, обобщающее понятие прямой (или отрезка прямой) евклидовой геометрии на случай пространств более общего вида. Определения Г. л. в различных пространствах зависят от того, какая из структур (метрика, линейный … Математическая энциклопедия
ЛИ ГРУППА ПРЕОБРАЗОВАНИЙ — гладкое действие связной группы Ли Gна гладком многообразии М, т. е. гладкое (класса ) отображение . такое, что: (е единица группы G). Ли г. п., удовлетворяющая также условию: наз. эффективной. Примеры Ли г. п. Любое гладкое линейное… … Математическая энциклопедия
Однопараметрическая подгруппа — группы Ли над нормированным полем аналитический гомоморфизм аддитивной группы поля в , то есть такое аналитическое отображение , что , для всех … Википедия
ЛИ РАЗРЕШИМАЯ ГРУППА — группа Ли, разрешимая как абстрактная группа. В дальнейшем рассматриваются вещественные или комплексные Ли р. г. Нильпотентная, в частности абелева, группа Ли разрешима. Если F={Vi} полный флаг в конечномерном векторном пространстве V(над или ),… … Математическая энциклопедия
ЛИ ЭКСПОНЕНЦИАЛЬНАЯ АЛГЕБРА — алгебра Ли типа (Е), конечномерная вещественная алгебра Ли для любого элемента Xк рой оператор присоединенного представления adX не имеет чисто мнимых собственных значений. Экспоненциальное отображение ехр : в соответствующую алгебре односвязную… … Математическая энциклопедия
ЛИ ЭКСПОНЕНЦИАЛЬНАЯ ГРУППА — группа Ли типа (Е), вещественная конечномерная группа Ли G, для к рой экспоненциальное отображение ехр: где алгебра Ли группы G, является диффеоморфизмом. Любая Ли э. г. разрешима, односвязна, а ее алгебра Ли является Ли экспоненциальной алгеброй … Математическая энциклопедия
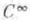 с аффинной связностью, р - нек-рая точка из М, М р - касательное пространство к многообразию Мв точке ри X - ненулевой вектор из
с аффинной связностью, р - нек-рая точка из М, М р - касательное пространство к многообразию Мв точке ри X - ненулевой вектор из 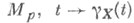 - геодезическая, проходящая через точку р в направлении вектора X. Существует такая открытая окрестность N0 точки 0 в М р и такая открытая окрестность N р точки рв М, что отображение
- геодезическая, проходящая через точку р в направлении вектора X. Существует такая открытая окрестность N0 точки 0 в М р и такая открытая окрестность N р точки рв М, что отображение  является диффеоморфизмом N0 на N р. Это отображение называется Э. о. в точке р и обозначается Ехр. Окрестность N0 наз. нормальной, если: 1) отображение Ехр диффеоморфно отображает N0 на N р,2) если
является диффеоморфизмом N0 на N р. Это отображение называется Э. о. в точке р и обозначается Ехр. Окрестность N0 наз. нормальной, если: 1) отображение Ехр диффеоморфно отображает N0 на N р,2) если  и
и 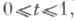 то
то 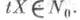 В этом случае N р - нормальная окрестность точки . в многообразии М. Каждая точка
В этом случае N р - нормальная окрестность точки . в многообразии М. Каждая точка 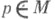 обладает выпуклой нормальной окрестностью N р точки р: любые две точки такой окрестности можно соединить в точности одним геодезич. отрезком, содержащимся в N р. Если М - полное риманово многообразие, то Ехр есть сюръективное отображение М р на М.
обладает выпуклой нормальной окрестностью N р точки р: любые две точки такой окрестности можно соединить в точности одним геодезич. отрезком, содержащимся в N р. Если М - полное риманово многообразие, то Ехр есть сюръективное отображение М р на М.  существует единственный аналитич. омоморфизм
существует единственный аналитич. омоморфизм 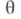 группы
группы 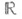 в Gтакой, что касательный вектор к
в Gтакой, что касательный вектор к 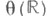 в точке есовпадает с X. Отображение
в точке есовпадает с X. Отображение  и наз. Э. о. алгебры gв группу G. Существует такая открытая окрестность N0 точки 0 в gи такая открытая окрестность N е точки ев G, что ехр является аналитич. диффеоморфизмом окрестности N0 на Ne. Пусть Х 1, ... , Х п - нек-рый базис алгебры g. Отображение
и наз. Э. о. алгебры gв группу G. Существует такая открытая окрестность N0 точки 0 в gи такая открытая окрестность N е точки ев G, что ехр является аналитич. диффеоморфизмом окрестности N0 на Ne. Пусть Х 1, ... , Х п - нек-рый базис алгебры g. Отображение 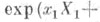
 есть система координат на Ne, эти координаты наз. каноническими.
есть система координат на Ne, эти координаты наз. каноническими. 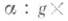
 Оказывается, что Э. о. ехр алгебры gв группу G совпадают с отображением Ехр касательного пространства gк многообразию . в точке ев это многообразие относительно лсвоинвариантной аффинной связности, отвечающей любой кососимметричной билинейной функции
Оказывается, что Э. о. ехр алгебры gв группу G совпадают с отображением Ехр касательного пространства gк многообразию . в точке ев это многообразие относительно лсвоинвариантной аффинной связности, отвечающей любой кососимметричной билинейной функции 
