ЦЕНТРИРОВАННОЕ СЕМЕЙСТВО МНОЖЕСТВ
- ЦЕНТРИРОВАННОЕ СЕМЕЙСТВО МНОЖЕСТВ
- семейство, пересечение любого конечного множества элементов к-рого не пусто. Напр., счетное семейство  состоящее из подмножеств натурального ряда чисел
состоящее из подмножеств натурального ряда чисел  вида
вида 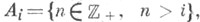 центрировано. Центрированным будет любое семейство, пересечение всех элементов к-рого не пусто. Этим свойством обладает любое конечное Ц. с. м.
центрировано. Центрированным будет любое семейство, пересечение всех элементов к-рого не пусто. Этим свойством обладает любое конечное Ц. с. м.
Впервые бесконечные Ц. с. м. были использованы в общей топологии для характеристики бикомпактных пространств. Ц. с. м., замкнутых в топологич. пространстве, используются при построении его бикомпактного расширения и его абсолюта.
Понятие Ц. с. м. допускает следующее обобщение. Пусть m - бесконечное кардинальное число. Тогда m-центрированным семейством: множеств наз. такое семейство, что пересечение любого множества его элементов мощности, меньшей т, не пусто. Такие семейства применяются для характеристики m-компактных пространств и в абстрактной теории меры.
Лит.:[1] Келли Дж., Общая топология, пер. с англ., 2 изд., М., 1981; [2] Gillman L., Jеrisоn M., Rings of continuons functions, Princeton. 1960.
Б. А. Ефимов.
Математическая энциклопедия. — М.: Советская энциклопедия.
И. М. Виноградов.
1977—1985.
Смотреть что такое "ЦЕНТРИРОВАННОЕ СЕМЕЙСТВО МНОЖЕСТВ" в других словарях:
Компактное пространство — определённый тип топологических пространств, включающий Все пространства с конечным числом точек; Все замкнутые и ограниченные подмножества евклидова пространства. В топологии компактные пространства по своим свойствам напоминают конечные… … Википедия
Бикомпактное пространство — Компактное пространство это топологическое пространство, в любом покрытии которого открытыми множествами найдётся конечное подпокрытие. В топологии, компактные пространства по своим свойствам напоминают конечные множества в теории множеств.… … Википедия
Компактное множество — Компактное пространство это топологическое пространство, в любом покрытии которого открытыми множествами найдётся конечное подпокрытие. В топологии, компактные пространства по своим свойствам напоминают конечные множества в теории множеств.… … Википедия
Локальная компактность — Компактное пространство это топологическое пространство, в любом покрытии которого открытыми множествами найдётся конечное подпокрытие. В топологии, компактные пространства по своим свойствам напоминают конечные множества в теории множеств.… … Википедия
Локально компактное пространство — Компактное пространство это топологическое пространство, в любом покрытии которого открытыми множествами найдётся конечное подпокрытие. В топологии, компактные пространства по своим свойствам напоминают конечные множества в теории множеств.… … Википедия
Ограниченно компактное пространство — Компактное пространство это топологическое пространство, в любом покрытии которого открытыми множествами найдётся конечное подпокрытие. В топологии, компактные пространства по своим свойствам напоминают конечные множества в теории множеств.… … Википедия
Относительная компактность — Компактное пространство это топологическое пространство, в любом покрытии которого открытыми множествами найдётся конечное подпокрытие. В топологии, компактные пространства по своим свойствам напоминают конечные множества в теории множеств.… … Википедия
Относительно компактное множество — Компактное пространство это топологическое пространство, в любом покрытии которого открытыми множествами найдётся конечное подпокрытие. В топологии, компактные пространства по своим свойствам напоминают конечные множества в теории множеств.… … Википедия
Предкомпакт — Компактное пространство это топологическое пространство, в любом покрытии которого открытыми множествами найдётся конечное подпокрытие. В топологии, компактные пространства по своим свойствам напоминают конечные множества в теории множеств.… … Википедия
Предкомпактное множество — Компактное пространство это топологическое пространство, в любом покрытии которого открытыми множествами найдётся конечное подпокрытие. В топологии, компактные пространства по своим свойствам напоминают конечные множества в теории множеств.… … Википедия
 состоящее из подмножеств натурального ряда чисел
состоящее из подмножеств натурального ряда чисел  вида
вида 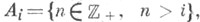 центрировано. Центрированным будет любое семейство, пересечение всех элементов к-рого не пусто. Этим свойством обладает любое конечное Ц. с. м.
центрировано. Центрированным будет любое семейство, пересечение всех элементов к-рого не пусто. Этим свойством обладает любое конечное Ц. с. м. 