ХОДЖА СТРУКТУРА

веса n (чистая) -объект, состоящий из решетки в действительном векторном пространстве н разложения комплексного векторного пространства (разложения Ходжа). При этом должно выполняться условие где черта означает комплексное сопряжение в Другое описание разложения Ходжа состоит в задании убывающей фильтрации (фильтрации Ходжа) в такой, что при Тогда подпространства 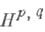восстанавливаются по формуле
Примером является Х. с. в пространстве n-мерных когомологий компактного кэлерова многообразия X, впервые изученная У. Хеджем (см. [1]). В этом случае подпространства описываются как пространства гармонических форм типа ( р, q )или как когомологий пучков голоморфных дифференциальных форм [2]. Фильтрация Ходжа в возникает из фильтрации комплекса пучков n-мерные гиперкогомологии к-рого изоморфны подкомплексами
Более общим понятием является смешанная Х. <с. Это -объект, состоящий из решетки в возрастающей фильтрации (фильтрации весов) W_n в и убывающей фильтрации (фильтрации Ходжа) F^p в таких, что на пространстве фильтрации F^p и определяют чистую Х. <с. веса п. Рассмотрена [3] смешанная Х. <с. в когомологиях комплексного алгебраич. многообразия (не обязательно компактного или гладкого), как аналог структуры модуля Галуа в этальных когомологиях. Х. <с. имеют важные приложения в алгебраич. геометрии (см. Отображение периодов )и в теории особенностей гладких отображений (см. [4]).

Лит.:[1] Ноdgе W. V. D., The theorie and applications of harmonic integrals, 2 ed., Camb., 1952; [2] Гриффите Ф., Харрис Дж., Принципы алгебраической геометрии, пер. с англ., т. 1, М., 1982; [3] Dе1ignе P., лProc. Intern. Congr. Math.