ХЕЛЛИ ТЕОРЕМА

- 1) X. т. о пересечении выпуклых множеств c общей точкой: пусть К - семейство из но менее чем n+1 выпуклых множеств в re-мерном аффинном пространство А ⁿ, причем К - конечно или каждое множество из К - компактно; тогда, если каждые n+1 из множеств семейства имеют общую точку, то существует точка, общая всем множествам семейства К.
X. т. посвящены многие исследования, относящиеся к ее приложениям, доказательству различных аналогов и предложений типа X. т., ее обобщений, напр. в вопросах чебышевского приближения, в решениях освещения задач, в теории выпуклых тел. Часто X. т. фигурирует в доказательствах комбинаторных утверждений следующего тина: если в нек-ром семействе каждое подсемейство из kчленов обладает определенным свойством, то этим свойством обладает и все семейство. Напр., осли аи b - две точки множества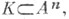 то выражение ла видно из bв К" обозначает, что отрезок [ а, b]принадлежит К. Пусть компакт 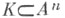обладает свойством, что для каждых п+1точек из Ксуществует точка в К, из к-рой видны эти точки, тогда в Ксуществует точка, из к-рой видны все точки К, т. е. К - звездное множество.
Большинство аналогов X. т. и ее обобщений связаны с различными вариантами понятия лвыпуклость