ФУНКЦИОНАЛЬНОЕ ИСЧИСЛЕНИЕ

гомоморфизм нек-рой алгебры функций Ав алгебру L(X)непрерывных линейных операторов в топологич. векторном пространстве X. Ф. и.-один из основных инструментов общего спектрального анализа и теории банаховых алгебр, к-рый позволяет использовать в этих дисциплинах функционально-аналитич. методы. Обычно A-топологическая (в частности, нормированная) алгебра функций на нек-ром подмножестве Кпространства 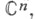содержащая многочлены переменных z¹, . .., zⁿ (часто К - плотное подмножество), так что Ф. и. 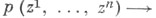является естественным продолжением полиномиального исчисления коммутирующих операторов 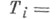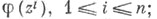в этом случае говорят, что набор Т =(T₁,.... Т _п )допускает А- исчисление, и пишут 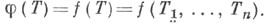А-исчисление для Т - это род спектральной теоремы, так как соответстви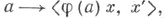е где 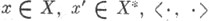-двойственность между Xи X*, определяет слабое операторно-значное А-распределение, перестановочное с Т.
Классическое Ф. и. Неймана - Мурье - Данфорда ( А=С (К), X - рефлексивное пространство) приводит к операторной (проекторной) спектральной мере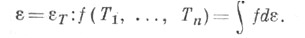

Ф. и. Рисса - Данфорда (n=1, 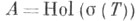-все функции, голоморфные на спектре 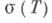оператора Т)приводит к формуле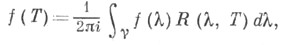

где 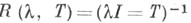-резольвента оператора,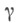- контур, охватывающий 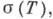вплоть до к-рого регулярна функция f. Формулы последнего типа для многих переменных (операторов) зависят от записи линейного функционала на 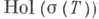и способа определения совместного спектра 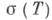набора Т= (Т ₁, ...,Т _n )(от определения 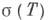зависит и объем Ф. и.).
Если Т - спектральный оператор, Sи N - его скалярная и квазинильпотентная части соответственно, а то формула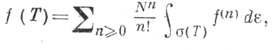

где 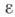-разложение единицы Т, позволяет распространить Ф. п. Рисса-Данфорда для . на более широкий класс функций. В частности, если 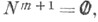то Тдопускает Ф. и. на классе раз непрерывно дифференцируемых функций. Если Т - оператор скалярного типа, то в эту формулу можно подставить ограниченные борелевские функции на 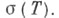В частности, такое Ф. и. допускают нормальные операторы в гильбертовом пространстве. Верно и обратное: если оператор Тдопускает Ф. и. (для операторов в рефлексивных пространствах достаточно предполагать существование Ф. и. на классе непрерывных функций), то Т- спектральный оператор скалярного типа (в гильбертовом пространстве - линейно подобный нормальному оператору).
Для операторов с достаточно медленным ростом резольвенты вблизи спектра построена [5] теория неаналитических С{M_k}-исчислений, опирающаяся на классы Карлемана и использующая формулу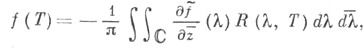

где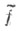 - т. н. 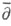-продолжение функции f за пределы спектра 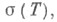т. о. финитная C¹ -функция в С, для которой

здесь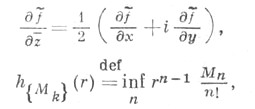

а оператор Тудовлетворяет условию

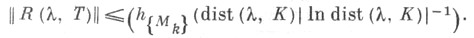
С другой стороны, более широкие (чем 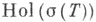исчисления возникают как следствия оценок операторных многочленов р(Т); напр., если X - гильбертово пространство, то неравенство Неймана - Хайнца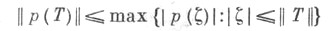

приводит к Ф. и. Сёкефальви-Надя-Фояша ( А- алгебра всех голоморфных и ограниченных в круге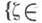 функций, Т - сжатие без унитарных частей), а оно - к многочисленным приложениям в теории функциональной модели для сжимающих операторов. Аналог неравенств Неймана - Хайнца для симметричных пространств функций порождает Ф. и. в терминах мультипликаторов (соответствующих сверточных пространств, [8]).
Применения. Тип Ф. и., допускаемый оператором Т, является инвариантом относительно линейного подобия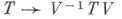 и успешно используется для классификации операторов. В частности, построена обширная теория т. н. А-скалярных операторов, применимая ко многим классам операторов, не укладывающихся в классическую спектральную теорию. Для успешного использования Ф. и. имеют значения т. н. теоремы об отображении спектра: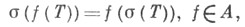

для всех перечисленных выше Ф. и. такие теоремы доказаны (после надлежащего осмысления правой части формулы).
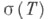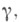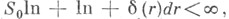Если алгебра Асодержит мелкие разбиения единицы (напр., то А- Ф. <и. позволяет построить локальный спектральный анализ и, в частности, доказать существование нетривиальных инвариантных подпространств оператора Т(если - не одноточечное множество); пример - оператор Т(в банаховом пространстве), спектр которого лежит на гладкой кривой и где 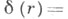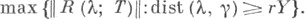Следствием локального анализа является и теорема Шилова об идемпотентах [2].

Лит.:[1] Данфорд Н., Шварц Дж., Линейные операторы, пер. с англ., ч. 1, М., 1962, ч. 3, М., 1974; [2] Бурбаки Н., Спектральная теория, пер. с франц., М., 1972; [3] Wаelbroeck L., Etude spectrale des algebres completes, Brux. 1960; [4] Тауlоr J. L., лActa math.