- СПЕКТР
оператора- совокупность
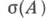чисел 
для к-рых оператор 
не имеет всюду определенного ограниченного обратного. Здесь А - линейный оператор в комплексном банаховом пространстве Х, I- тождественный оператор в X. Если Ане замкнут в X, то 
поэтому обычно рассматривают С. замкнутых операторов (для операторов, допускающих замыкание, иногда их С. наз. спектр замыкания).
Если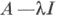
не инъективен или не сюръективен, то 
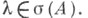В первом случае 
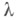наз. собственным значением оператора А; совокупность 
собственных значений наз. точечным спектром. Во втором случае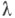 
наз. точкой непрерывного спектра 
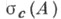или остаточного спектра 
в зависимости от того, плотно или не плотно в Xподпространство 
Существуют и другие классификации точек С., напр.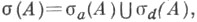
где 
состоит из aппpoкcимативных собственных значений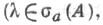 
если существуют 
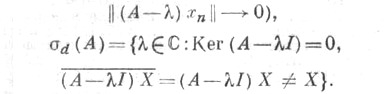
При атом
и, значит, 
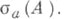В теории возмущений рассматривается предельный спектр 
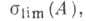состоящий из предельных точек 
и изолированных собственных значений бесконечной кратности, вейлевский спектр, равный пересечению С. всех компактных возмущений, и др.
Если оператор Аограничен, то
компактен и не пуст (в этом случае 
совпадает со спектром элемента Абанаховой алгебры В(X)); в общем случае можно утверждать лишь, что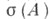 
замкнут в 
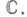На множестве 
определена аналитическая В(Х)-значная функция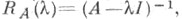 
наз. резольвентой 
наз. резольвентным множеством). С помощью резольвенты строится функциональное исчисление от оператора Ана функциях, аналитических в окрестности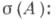 
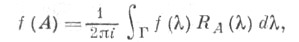
где Г - контур, охватывающий
(неограниченность Анакладывает на выбор Г нек-рые ограничения); дополнительные условия на геометрию С. и асимптотику резольвенты позволяют расширить это функциональное исчисление.
С. функций от оператора определяются формулой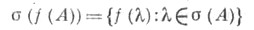
(теорема об отображении спектра); s (A*) сопряженного оператора совпадает с
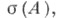если Аограничен, а в общем случае 
Если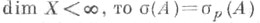
и X раскладывается в прямую сумму инвариантных относительно . подпространств, в каждом из к-рых Аиндуцирует оператор с одноточечным С.; поисками бесконечномерных аналогов такого разложения занимается спектральная теория операторов. См. также Спектральный анализ, Спектральный синтез, Спектральный оператор, Спектральное разложение. Лит.:[1] Данфорд H., Шварц Дж., Линейные операторы. Общая теория, пер. с англ., т. 1, М., 1962; [2] КатоТ., Теория возмущений линейных операторов, пер. с англ., М., 1972.
В. С. Шулъман.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
