ФУБИНИ ФОРМА

- дифференциальная форма (квадратичная F₂ и кубическая F₃),на основе к-рой строится проективная дифференциальная геометрия. Введены Г. Фубини (см. [1]).
Пусть - (однородные) проективные координаты точки поверхности с внутренними координатами u¹, u² и пусть

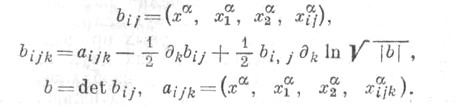
Тогда Ф. ф. определяются так:

Однако сами проективные координаты не вполне определены: они допускают введение произвольных множителей и однородных линейных преобразовании. Поэтому Ф. ф. определены только с точностью до множителя и чтобы избежать связанных с этим затруднений, нормируют координаты и определенные через них формы; напр., при унимодулярных проективных преобразованиях Ф. ф. сохраняют свое значение (с точностью до знака). Отношение F₃/F₂,наз. проективным линейным элементом, уже не зависит от нормирования (и определяет проективный метрич. элемент) .
Построенные метрич. средствами, исходя из второй квадратичной формы и формы Дарбу (определяемой Дарбу тензором),Ф. ф.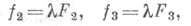

инварианты относительно эквиаффинных преобразований и потому могут быть положены в основу эквиаффинной дифференциальной геометрии.

Лит.:[1] Fubini G., Cech E., Geometria proiettiva differenzial, v. 1-2, Bologna, 1926-27; [2] Каган В. Ф., Основы теории поверхностей..., т. 2, М.-Л., 1948; [3] Широков П. А., Широков А. П., Аффинная дифференциальная геометрия, М., 1959.
М. И. Войцеховский.