ДИФФЕРЕНЦИАЛЬНАЯ ФОРМА

- 1) Д. ф. степени р, р - форма на дифференцируемом многообразии М- р раз ковариантное тензорное поле на М. Ее можно интерпретировать также как р-линейное (над алгеброй F(M)гладких вещественных функций на М)отображение 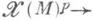F(M), где есть Р(М) -модуль гладких векторных полей на М. Формы степени 1 наз. также пфаффовыми формами. Примером такой формы является дифференциал df гладкой функции fна М, определяемый следующим образом: (df)(X), есть производная Xf функции f по направлению поля X. Римановы метрики на многообразии Мслужат примерами симметрических Д. ф. степени 2. Часто, однако, термин "Д. ф." относят к кососимметрическим, или внешним Д. ф., имеющим наибольшее число приложений.

Если (х ¹, ..., х ⁿ) - локальная система координат в области то формы dx¹,. . ., dxⁿ составляют базис в кокасательном пространстве Т _x (М)*, Поэтому (см. Внешняя алгебра )любая внешняя р- форма a. записывается в Uв виде

где а,-, ,Х - функции в U. В частности,

Пусть Е ^Р=Е ^Р (М).- пространство всех внешних р- форм класса С°°, причем E⁰(M)=F(M). Внешнее умножение превращает(где n=dim M)в ассоциативную градуированную алгебру над F(M), удовлетворяющую условию градуированной коммутативности

Гладкое отображение многообразий порождает гомоморфизм алгебр над R.

Понятие дифференциала функции обобщается следующим образом. Для всякого существует единственное линейное отображение d: (внешний дифференциал), совпадающее при р=0с введенным выше дифференциалом и обладающее свойствами:

Внешний дифференциал формы а, записанной в локальных координатах в виде (1), выражается формулой

Его бескоординатная запись:

где Оператор взятия Ли производной L_X,на Д. ф. связан с внешним дифференциалом соотношением

где t_X :- оператор внутреннего умножения на X:

Оператор dпревращает Е* (М)в коцепной комплекс (комплекс де Рама). Коциклы этого комплекса наз. замкнутыми формами, кограницы - точными формами. Согласно де Рама теореме, алгебра когомологий

комплекса де Рама изоморфна алгебре Н* ( М,R.) вещественных когомологий многообразия М. В частности, H^P(Rⁿ) =0 при р>0 (лемма Пуанкаре). С теоремой де Рама тесно связана другая операция - интегрирование Д. ф. Пусть D- ограниченная область в R^p, s- гладкое отображение определенное в окрестности замыкания D. Если то где а- гладкая функция в D. Интеграл формы a по поверхности s определяется формулой

Если Dимеет кусочно гладкую границу, то справедлива формула

где определяется как сумма интегралов формы a по гладким кускам границы, снабженных естественными параметризациями. Частными случаями этой формулы являются классич. формулы Ньютона - Лейбница, Грина, Гаусса - Остроградского, Стокса (см. также Стокса теорема). В силу формулы (3) каждая замкнутая р-форма a. определяет р-мерный сингулярный коцикл, значение к-рого на симплексе s

равно Это соответствие как раз и реализует изоморфизм из теоремы де Рама.

Формула (3) была опубликована в 1899 А. Пуанкаре (см. [2]), к-рый рассматривал внешние формы как подинтегральные выражения для образования интегральных инвариантов. Одновременно Э. Картан (см. [3]) дал близкое к современному определение внешних форм и внешнего дифференциала (вначале на пфаффовых формах), подчеркнув связь своей конструкции с внешней алгеброй.

Наряду с определенными выше скалярными внешними формами можно рассматривать внешние Д. ф. со значениями в векторном пространстве Vнад R. Если Vявляется алгеброй, то в пространстве Е( М, V )форм со значениями в Vопределено естественное умножение (обобщение внешнего умножения). Если при этом алгебра V-ассоциативна, то и Е( М, V )ассоциативна; если Vкоммутативна, то Е( М, V). градуированно-коммутативна (формула (2)); если V- алгебра Ли, то Е( М, V)- градуированная алгебра Ли. Часто рассматривается также следующее, еще более общее понятие. Пусть F- гладкое векторное расслоенное пространство с базой М. Если сопоставить каждой точке хО М кососимметрическую р-линейную функцию на Т _x (М)со значениями в слое F_x расслоения F, то получится так наз. F-значная р-форма. F-значную р-форму можно интерпретировать также как р-линейное (над F(M))отображение модуля в модуль гладких сечений расслоения F. Пространство таких форм обозначается Е ^р(F). Если Fзадано локально постоянными функциями перехода или, что то же, в F задана плоская связность, то можно корректно определить комплекс де Рама и обобщить теорему де Рама на этот случай.

Формы со значениями в касательном расслоении Т(М)наз. также векторными Д. ф.; векторные р-формы можно отождествить с р раз ковариантными и 1 раз контравариантными тензорными полями на М, кососимметричными по ковариантным индексам. С помощью векторных Д. ф. описываются дифференцирования алгебры внешних форм Е(М)[4]. Векторные формы (а также их обобщение - струйные формы) находят применение в теории деформаций комплексных и других дифференциально-геометрич. структур на многообразиях.

продолжение Дифференциальная форма....

Аналоги Д. ф. можно построить также в симплициальной теории. Одна из таких конструкций, восходящая к X. Уитни [5], может быть использована для вычисления рациональных когомологий симплициального комплекса K. Кусочно линейной формой (или PL -формой) на K наз. согласованный набор Д. ф., заданных на симплексах комплекса Ки имеющих в качестве коэффициентов при записи в барицентрич. координатах многочлены с рациональными коэффициентами. PL -формы на Кобразуют градуированно-коммутативную дифференциальную алгебру E*_pl(K)над Q. Интегрирование форм определяет изоморфизм алгебры когомологий этой алгебры на алгебру Н*(|K|,Q), где | К| -полиэдр, отвечающий комплексу К. Алгебра E*_PL(K)полностью определяет также рациональный гомотопич. тип (в частности, ранги гомотопич. групп) пространства | К|. Аналогично алгебра Е* (М)на дифференцируемом многообразии Мопределяет его вещественный гомотопич. тип [9].

Исчисление внешних форм на комплексном аналитич. многообразии имеет ряд особенностей [6]. В этой ситуации обычно рассматриваются пространства ЕР( М, С) комплекснозначных форм или пространства EP(F), где F.- голоморфное векторное расслоение на М. Имеет место разложение

где E^{r, s}(M)- пространство форм типа (r, s), т. е. форм а, локально представимых в виде

где (z¹, . .., zⁿ) - локальная аналитич. система координат на М. Аналогично

При этом d'=d"=0, так что d' и d" определяют коцепные комплексы. Наиболее известен комплекс оператора d" (комплекс Дольбо), когомологий к-рого обозначаются через H^r,s(M). d" -коциклы типа (р, 0) суть голоморфные р-формы (см. Голоморфная форма). Для d" справедлива, следующая лемма Гротендика: если а- форма типа (r, s )с s>0 в окрестности нуля пространства С" и d"a=0, то в меньшей окрестности нуля существует такая форма b типа (r, s-1), что a=d"b. Комплекс Дольбо можно определить также и для F-значных форм, где F- голоморфное векторное расслоение. Это приводит к пространствам когомологий H^{r, s}(F). Из леммы Гротендика вытекает следующий изоморфизм:

где Q^r(F)- пучок ростков голоморфных F-значных r-форм (теорема Дольбо). В частности,

где Q^r (М)- пучок ростков голоморфных r-форм на М. Существует спектральная последовательность с первым членом сходящаяся к H*( М, С).

Эйлерова характеристика Х(М)компактного комплексного многообразия Мвыражается через когомологий Дольбо по формуле

Д. ф. являются важной составной частью аппарата дифференциальной геометрии (см. [7], [8]). Они систематически используются также в топологии, теории дифференциальных уравнений, механике, теории комплексных многообразий и функций многих комплексных переменных. Обобщением Д. ф., аналогичным обобщенным функциям, являются потоки. Алгебраич. аналог теории Д. ф. (см. Дифференциалов модуль )позволяет определить дифференциальные формы на алгебраических многообразиях и на аналитических пространствах (см. Дифференциальное исчисление на аналитических пространствах). См. также Рама когомологий, Дифференциал на римановой поверхности, Гармоническая форма, Голоморфная форма, Лапласа оператор.

Лит.:[1] де Рам Ж., Дифференцируемые многообразия, пер. с франц., М., 1956; [2] Роinсаre Н., Les methodesaouvelles de la mgcanique celeste, t. 3, P., 1899; [3] Gartan E., (Euvres completes, pt. 2, t. 1, p. 303-96; [4] Froliсher A., Nijenhuis A.,"Proc. Koninkl. ned. akad. wet.", Ser. A, 1956, v. 59, № 3, p. 338-59; [5] Уитни X., Геометрическая теория интегрирования, пер. с англ., М., 1960; [6] Уэллс Р., Дифференциальное исчисление на комплексных многообразиях, пер. с англ., М., 1976; [7] Стернберг С, Лекции по дифференциальной геометрии, пер. с англ., М., 1970; [8] Картан А., Дифференциальное исчисление. Дифференциальные формы, пер. с франц., М., 1971; [9] Грифитс Ф. [и др.], "Успехи матем. наук", 1977, т. 32, в. 3, с. 119-52.

А. Л. Онищик.

2) Д. ф. на алгебраическом многообразии - аналог понятия дифференциальной формы на дифференцируемом многообразии. Пусть X - неприводимое алгебраич. многообразие размерности dнад алгебраически замкнутым полем k, К- его поле рациональных функций. Дифференциальной формой степени r на Х наз. элемент К- пространства

где W_K/k- дифференциалов модуль поля Кнад полем k. Если x₁, ..., х _d- сепарабельный базис трансцендентности расширения К/k, то каждая Д. ф. записывается в виде

где Д. ф. w наз. регулярной на открытом множестве если со принадлежит подмодулю W^r_k[U]/k пространства W^r(X), рассматриваемого как модуль над кольцом k[U]регулярных функций на подмножестве U. Д. ф. со наз. регулярной, если любая точка имеет такую окрестность V, что со регулярна на U. Регулярные Д. ф. на Xобразуют модуль над k[Z], обозначаемый W^r[X]. Его элемепты отождествляются с сечениями пучка W^r_X/k на многообразии X. В окрестности любой точки регулярная Д. ф. записывается в виде

где функции a_i1...ir, f_i1, ... , f_ir регулярны в точке х. Если X- полное многообразие, то пространства W^r[Х] конечномерны, а в случае, когда Xнеособое, размерность наз. геометрическим родом многообразия X. В случае, когда X- полное многообразие над полем комплексных чисел, пространство W^r[X] совпадает с пространством голоморфных Д. ф. степени rна соответствующем аналитич. ространстве Х ^ап.

Пусть X- нормальное многообразие и для любой точки коразмерности 1 Д. ф. со может быть записана в виде

где апринадлежит полю частных К _х локального кольца , t- образующая его максимального идеала, t₁, ..., t_d-1- сепарабельный базис трансцендентности над кполя вычетов кольца Q_{X, х}. Значение нормирования на элементе а, определяемое кольцом Q_{X, х}, не зависит от выбора представления w в виде (*) и обозначается v_x(w). Дивизор

определен и наз. дивизором дифференциальной формы со. Д. ф. со регулярна тогда и только тогда, когда ее дивизор , т. е. для всех Дивизоры любых двух Д. ф. эквивалентны, более того, дивизоры всех Д. ф. на данном алгебраич. многообразии образуют класс дивизоров относительно линейной эквивалентности. Этот класс наз. каноническим классом многообразия X иобозначается через К _X- Для неособого многообразия Xкласс К _X совпадает с первым классом Чженя обратимого пучка - в частности

для любого

Для любого доминантного рационального отображения алгебраич. многообразий определен канонич. гомоморфизм

При этом, если Xи X'- неособые, а X- полное, то f* переводит регулярные Д. ф. в регулярные. В частности, если неособые полные многообразия Xи X' бирационально изоморфны, то векторные пространства W^r[X] и W^r[X'] изоморфны над полем k.

Для любого г>1 элементы i-й симметрич. степени Sⁱ(W^r(X)) K -пространства W^r(X)наз. i-кратными дифференциальными формами степени г на X. Каждую такую Д. ф. можно рассматривать как рациональное сечение пучка Sⁱ(W^r_X/k). Регулярные сечения

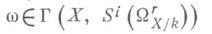
наз. регулярными i-к ратными дифференциальными формами степени rна X. Для неособого полного многообразия X размерность наз. i-родом многообразиях. Для бирационально изоморфных многообразий их i-роды совпадают. Лит.:[1] Шафаревич И. Р., Основы алгебраической геометрии, М., 1972; [2] Бальдассарри М., Алгебраические многообразия, пер. с англ., М., 1961. И. В. Долгачев.