ФАКТОРНОЕ ОТОБРАЖЕНИЕ

- отображение f то пологич. пространства Xна топологич. пространство Y, при к-ром множество 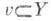открыто в пространстве Yв том и только том случае, если его прообраз f^-1v открыт в пространстве X. Если дацрэ отображение f топологич. пространства Xна множество Y, то на Yсуществует сильнейшая топология (т. е. содержащая наибольшее число открытых множеств) среди всех топологий, по отношению к к-рым отображение f непрерывно. Топология состоит из всех множеств таких, что множество f^-lvоткрыто в X. Топология является единственной среди всех топологий на множестве Yтакой, что f является Ф. <о. Поэтому топология наз. фактортопологией, отвечающей отображению f и топологиии 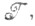заданной на Х.
Описанная выше конструкция возникает при рассмотрении разбиений топологич. пространств и приводит к важной операции-переходу от данного топологич. пространства к новому-пространству разбиения. Пусть дано разбиение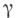 топологич. пространства 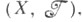т. е. семейство непустых попарно непересекающихся подмножеств множества X, покрывающее X. Тогда определено отображение проектировании 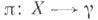правилом: 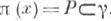, если 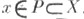Множество теперь наделяется фактортопологией отвечающей топологии на Xи отображению и топологич. пространство 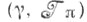на. <ч. пространством разбиения пространства Так, с точностью до гомеоморфизма окружность представляется какпространство разбиения отрезка, сфера -как пространство разбиения круга, лист Мёбиуса - как пространство разбиения прямоугольника, проективная плоскость - как пространство разбиения сферы и т. д.
Важны следующие свойства Ф. <о., связанные с рассмотрением диаграмм. Пусть -непрерывное отображение, причем f(X)=Y. Тогда существует топологнч. пространство Z, Ф. <о. 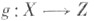и непрерывное взаимно-однозначное отображение (т. е. уплотнение) такое, что В качестве Zможно взять пространство разбиения пространства Xна полные прообразы точек при f, а в роли отображения g выступит тогда проектирование 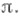Пусть даны непрерывное отображение и Ф. <о. причем выполняется условие: если 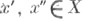и f ₁(x') =f₁(x"), то и f₂ (x') = f₂( х"). Тогда однозначно определенное отображение 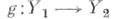такое, что оказывается непрерывным отображением. Сужение Ф. <о. на подпространство может не быть Ф. <о.- даже если это подпространство одновременно открыто и замкнуто в исходном пространстве. Декартово произведение Ф. <о. на тождественное отображение может не быть Ф. <о. Декартов квадрат Ф. <о. также может не быть Ф. <о. Сужение Ф. <о. на полный прообраз не обязано быть Ф. <о. Точнее, если есть Ф. <о. и то отображение может не быть факторным. Такого не может произойти, если подпространство Y₁ открыто или замкнуто в Y.
Эти факты показывают, что с Ф. о. надо обращаться осторожно и что с точки зрения теории категорий класс Ф. о. не столь гармоничен и удобен, как классы непрерывных отображений, совершенных отображений и открытых отображений. Однако рассмотрение пространств разбиений и отмеченные выше лдиаграммные