ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ

класс элементарных функций: синус, косинус, тангенс, котангенс, секанс, косеканс. Обозначаются соответственно: sin x,cos x, tg x,ctg x, sec x,cosec x.
Тригонометрические функции действительного аргумента. Пусть А - точка окружности с центром в начале координат и радиусом, равным единице,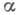 - угол между осью абсцисс и вектором ОА, отсчитываемый от положительного направления оси абсцисс (рис. 1). При этом если отсчет ведется против часовой стрелки, то величина угла считается положительной, а если по часовой стрелке - отрицательной, т. е. 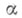- полярный угол точки А.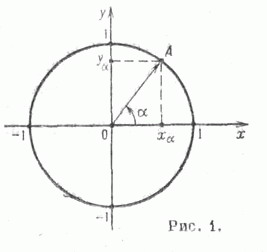

Если 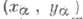- прямоугольные декартовы координаты точки А, то Т. ф. синус и косинус определяются формулами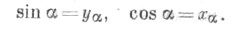

Остальные Т. ф. могут быть определены формулами

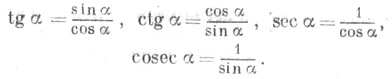
Все Т. ф.- периодические функции. Графики Т. ф. даны на рис. 2.

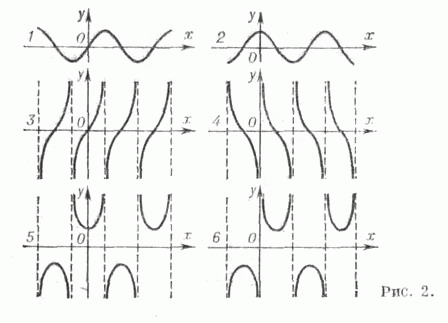Основные свойства Т. ф.: область определения, множество значений, четность и участки монотонности приведены в табл.

Функция	Область определения	Множество значений	Четность	Участки монотонности
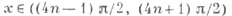sinx		[-1, +1]	нечетная	возрастает при .... ... убывает при
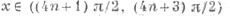cosx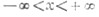		[-1, +1]	четная	возрастает при убывает при
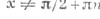
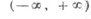tg x			нечетная	возрастает при
ctg x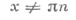			нечетная	убывает при
sec x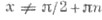			четная	возрастает при убывает при
соsес x	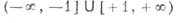		нечетная	возрастает при убывает при

Каждая Т. ф. в каждой точке своей ооласти определения непрерывна и бесконечно дифференцируема; производные Т. ф.:

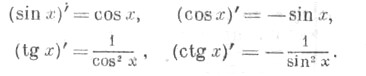
Интегралы от Т. ф.:

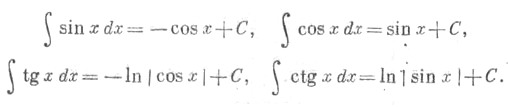
Все Т. ф. допускают разложение в степенные ряды:

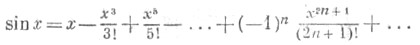
при

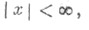
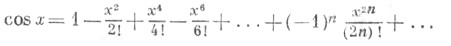
при

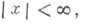
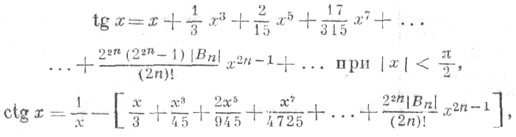
при 0 < |х|< (B_n - числа Бернулли).
Функция y=sinx, являющаяся обратной по отношению к функции z=sin у, определяет . как многозначную функцию от х', она обозначается y=Arcsin x. Аналогично определяются функции, обратные по отношению к другим Т. ф.; все они наз. обратными тригонометрическими функциями.
Тригонометрические функции комплексного переменного. Т. ф. для комплексных значений переменного z=x+iy определяются как аналитические продолжения соответствующих Т. ф. действительного переменного в комплексную плоскость.
Так, sinz и cosz можно определить с помощью рядов для sinxи cos х. Эти ряды сходятся во всей плоскости, поэтому sinz и cosz- целые функции.
Т. ф. тангенс и котангенс определяются формулами

Т. ф. tg z и ctg z - мероморфнае функции. Полюсы tg zпростые (1-го порядка) и находятся в точках полюсы ctg z также простые и находятся в точках
Все формулы, справедливые для Т. ф. действительного аргумента, остаются справедливыми и для комплексного аргумента.
В отличие от Т. ф. действительного переменного, функции sin zи cos z принимают все комплексные значения: уравнения sin z=a и cos z=a имеют решения для любого комплексного а:

Т. ф. tg z и ctg z принимают все комплексные значения, кроме уравнения tg z=o, ctg z=a имеют решения для любого комплексного числа

Т. ф. можно выразить через показательную функцию:

и гиперболические функции:sin z=-.sh iz, cos z=chiz, tg z =- i th iz.

В. И. Битюцков.