- ТРИГОНОМЕТРИЧЕСКАЯ СУММА
- конечная сумма Sвида
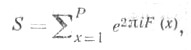
где
 Р - целое число, F(х) - действительная функция х. Т. с. также наз. и более общие суммы S' вида
Р - целое число, F(х) - действительная функция х. Т. с. также наз. и более общие суммы S' вида 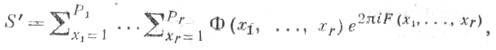
где F(х 1, . .., xr) -действительная функция, а Ф(x1, . . ., х r) - произвольная комплекснозначная функция.
Если F(x)- многочлен, то . наз. суммой Вейля; если многочлен F(х)имеет вид
то Sназ. рациональной тригонометрич. суммой; если P=q, то Sназ. полной тригонометрич. суммой; если r=1, Ф(x1)=1 при простом x1,и Ф(x1)=0 при составном x1, то Sназ. тригонометрич. суммой с простыми числами; если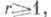 Ф (x1, . .., , xr)=1, F(x1, . .., , xr)- многочлен, то S' наз. кратной суммой Вейл я. Основной проблемой в теории Т. с. является проблема разыскания верхней грани модуля Sи S'.
Ф (x1, . .., , xr)=1, F(x1, . .., , xr)- многочлен, то S' наз. кратной суммой Вейл я. Основной проблемой в теории Т. с. является проблема разыскания верхней грани модуля Sи S'. Лит.:[1]Виноградов И. М., Избр. тр., М., 1952; [2] его же, Метод тригонометрических сумм в теории чисел, М., 1971; [3] его же, Особые варианты метода тригономстрических сумм, М., 1976; [4] Xуа Ло-ген, Метод тригонометрических сумм и его применения в теории чисел, пер. с нем., М., 1964; [5] Титчмарш Е. К., Теории дзета-функции Римана, пер. с англ., М., 1953; [6] Архипоп Г. И., Карацуба А. А., Чубариков В. Н., Кратные тригонометрические суммы, М., 1980.
А. А. Карацуба.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
