СУММИРУЕМОСТИ МНОЖИТЕЛИ — числовые множители (для членов ряда), преобразующие ряд суммируемый суммирования методом А, в ряд суммируемый методом В. В этом случае С. м. наз. множителями суммируемости типа ( А, B). Напр., числа являются С. м. типа ((с, k),( с, k s ))(см.… … Математическая энциклопедия
Бесконечное произведение — произведение бесконечного числа сомножителей u1, u2,..., un,..., т. е. выражение вида Б. п., в котором сомножителями являются числа, иногда называемые бесконечным числовым произведением. Б. п. не всегда может быть… … Большая советская энциклопедия
ОРТОГОНАЛЬНЫЙ РЯД — ряд вида где ортонормированная система функций (онс) относительно меры : Начиная с 18 в. при изучении различных вопросов математики, астрономии, механики и физики (движение планет, колебание струн, мембран и др.) в исследованиях Л. Эйлера (L.… … Математическая энциклопедия
НОРМАЛЬНАЯ ФОРМА — 1) Н. ф. матрицы A матрица Nзаранее определенного специального вида, получаемая из Ас помощью преобразований определенного типа. В зависимости от рассматриваемого типа преобразований, от области K, к к рой принадлежат коэффициенты А , от вида Аи … Математическая энциклопедия
Метод квадратичных форм Шенкса — метод факторизации целых чисел, основанный на применении квадратичных форм, разработанный Даниелем Шенксом (англ. Daniel Shanks).[1] в 1975 году, как развитие метода факторизации Ферма. Для 32 разрядных компьютерах алгоритмы, основанные на… … Википедия
БЕСКОНЕЧНОЕ ПРОИЗВЕДЕНИЕ — выражение содержащее бесконечное множество числовых или функциональных сомножителей, каждый из к рых отличен от нуля. Б. п. наз. сходящимся, если существует отличный от нуля предел последовательности частичных произведений при . 3начением Б. п.… … Математическая энциклопедия
Физическая астрономия — так называлась со времен Кеплера совокупность сведений и теорий о строении и действительном движении в пространстве небесных светил в противоположность сферической астрономии, изучающей видимое для нас положение светил на фиктивной небесной сфере … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
БЛЯШКЕ ПРОИЗВЕДЕНИЕ, — Бляшке функция, регулярная аналитич. функция комплексного переменного z, определенная в единичном круге в виде конечного пли бесконечного произведения где n целое неотрицательное число, последовательность точек такая, что произведение в правой… … Математическая энциклопедия
Математика — I. Определение предмета математики, связь с другими науками и техникой. Математика (греч. mathematike, от máthema знание, наука), наука о количественных отношениях и пространственных формах действительного мира. «Чистая … Большая советская энциклопедия
Целая функция — функция, голоморфная во всей комплексной плоскости. Типичным примером целой функции может служить многочлен или экспонента, а также суммы, произведения и суперпозиции этих функций. Ряд Тейлора целой функции сходится во всей плоскости комплексного … Википедия
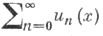- числа 
п=0,1, 2, . . ., такие, что ряд 
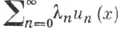сходится почти всюду на измеримом множестве X, где и п (х) - числовые функции, определенные на X. 
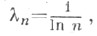п=2, 3, ...
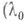и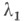 
можно выбрать произвольно), то есть есл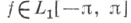и 
и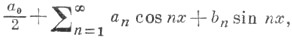 
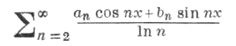
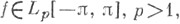то ее тригонометрич. ряд Фурье уже сам" сходится почти всюду (см. Карлесона теорема). 