- БЛЯШКЕ ПРОИЗВЕДЕНИЕ,
Бляшке функция,- регулярная аналитич. функция комплексного переменного z, определенная в единичном круге

 в виде конечного пли бесконечного произведения
в виде конечного пли бесконечного произведения 
где n - целое неотрицательное число,
 - последовательность точек
- последовательность точек  такая, что произведение в правой части (*) сходится (условие сходимости необходимо лишь в случае бесконечного произведения). В. п. было введено В. Бляшке [1], установившим следующее утверждение: последовательность
такая, что произведение в правой части (*) сходится (условие сходимости необходимо лишь в случае бесконечного произведения). В. п. было введено В. Бляшке [1], установившим следующее утверждение: последовательность 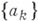 точек
точек  определяет функцию вида (*) тогда и только тогда, когда сходится ряд
определяет функцию вида (*) тогда и только тогда, когда сходится ряд 
 Каждый множитель вида
Каждый множитель вида

наз. множителем Бляшке для
 , осуществляет однолистное конформное отображение круга Кна себя, переводящее точку
, осуществляет однолистное конформное отображение круга Кна себя, переводящее точку  в нуль, с нормировкой
в нуль, с нормировкой  Множители вида
Множители вида  можно интерпретировать как множители Бляшке, соответствующие нулю
можно интерпретировать как множители Бляшке, соответствующие нулю  и нормировке
и нормировке  . Определение множителей Бляшке и Б. <п. легко переносится на круг произвольного радиуса, а также на любую одно-связную область, конформно эквивалентную кругу.
. Определение множителей Бляшке и Б. <п. легко переносится на круг произвольного радиуса, а также на любую одно-связную область, конформно эквивалентную кругу.
Последовательность
 (здесь n нулей), обычно выписываемая в порядке неубывания
(здесь n нулей), обычно выписываемая в порядке неубывания  , является последовательностью всех нулей Б. п. (*) (каждый нуль выписывается столько раз, какова его кратность). Таким образом, сформулированное выше утверждение Бляшке описывает те последовательности, к-рые являются последовательностями нулей всевозможных Б. п. Произведение (*) можно рассматривать как простейшую ограниченную голоморфную в круге Кфункцию, имеющую заданную последовательность нулей. Оно сходится абсолютно и равномерно внутри К, представляет в круге Кограниченную голоморфную функцию,
, является последовательностью всех нулей Б. п. (*) (каждый нуль выписывается столько раз, какова его кратность). Таким образом, сформулированное выше утверждение Бляшке описывает те последовательности, к-рые являются последовательностями нулей всевозможных Б. п. Произведение (*) можно рассматривать как простейшую ограниченную голоморфную в круге Кфункцию, имеющую заданную последовательность нулей. Оно сходится абсолютно и равномерно внутри К, представляет в круге Кограниченную голоморфную функцию,  почти всюду имеет угловые граничные значения, но модулю равные 1. Для того чтобы ограниченная голоморфная функция
почти всюду имеет угловые граничные значения, но модулю равные 1. Для того чтобы ограниченная голоморфная функция  была Б. п., необходимо и достаточно, чтобы выполнялось условие
была Б. п., необходимо и достаточно, чтобы выполнялось условие

С помощью Б. <п. удается дать факторизационное описание важных классов голоморфных функций в единичном круге K. Так, доказана следующая теорема Бляшке: последовательность
 точек круга Кявляется последовательностью всех нулей некоторой ограниченной голоморфной в Кфункции
точек круга Кявляется последовательностью всех нулей некоторой ограниченной голоморфной в Кфункции 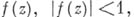 тогда и только тогда, когда ряд
тогда и только тогда, когда ряд  сходится. При этом
сходится. При этом  представима в виде произведения
представима в виде произведения  где
где  - Б. <п., построенное по нулям
- Б. <п., построенное по нулям  функции
функции  , а
, а  - отличная от нуля голоморфная в Кфункция,
- отличная от нуля голоморфная в Кфункция,  , допускающая сравнительно простое интегральное представление. Кроме ограниченных функций, аналогичное факторизационное описание строится для ограниченного вида функций, Харди классов (см. [2] -[4]).
, допускающая сравнительно простое интегральное представление. Кроме ограниченных функций, аналогичное факторизационное описание строится для ограниченного вида функций, Харди классов (см. [2] -[4]).
Изложенная теория получила существенное обобщение в работах М. М. Джрбашяна (см. [5], [6]), построившего бесконечные произведения более общей природы, пригодные для факторизации гораздо более широких классов мероморфных функций. Решена также задача построения аналогов Б. и. и теоремы Бляшке для двусвязных [7] и, вообще, конечносвязных [8] областей. Решение проблемы построения удобных аналогов Б. <п. для голоморфных функций многих комплексных переменных чрезвычайно затруднено тем обстоятельством, что нули таких функций не могут быть изолированными.
Лит.:[l] Btaschke W., "Ber. Verhandl Sachsisch. Akad Wiss. Leipzig. Math.-naturwiss. Kl". 1915, Bd 67, S. 194-200; [2] Пpивалов И. И., Граничные свойства аналитических функций, 2 изд., М.- Л., 1950; [3] Неванлинна Р., Однозначные аналитические функции, пер. с нем., М.- Л., 1941; [4] Коллингвуд Э., Ловатер Д ж., Теория предельных множеств, пер. с англ., М., 1971; [5] Джрбашян М. М., Интегральные преобразования и представления функций в комплексной области, М., 1966; [6] его же, "Успехи матем. наук", 1973, т. 28, в. 4 (172), с. 3-14; [7] Касьянюк С. А., "Матем. сб.", 1957, т. 42 (84), №3, с. 301-26; [8] Тамразов П. М., "Докл. АН СССР", 1965, т. 161, № 2, с. 308-11.
П. М. Тамразов.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
