- СФЕРА
- множество Sn точек хевклидова пространства En+1, находящихся от нек-рой точки х 0 (центр С.) на постоянном расстоянии R (радиус С.), т. е.

С. S0 - пара точек, С. S1 - это окружность, С. Sn при n>2 иногда наз. гиперсферой. Объем С. Sn (длина при п=1, поверхность при n=2) вычисляется по формуле

в частности,

Уравнение С. Sn в декартовых прямоугольных координатах в Е n+1 имеет вид

(здесь
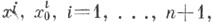 - координаты х, х0 соответственно), т. е. С.- (гипер)квадрика, или поверхность второго порядка специального вида.
- координаты х, х0 соответственно), т. е. С.- (гипер)квадрика, или поверхность второго порядка специального вида.
Положение какой-либо точки в пространстве относительно С. характеризуется степенью точки. Совокупность всех С., относительно к-рых данная точка имеет одинаковую степень, составляет сеть С. Совокупность всех С., относительно к-рых точки нек-рой прямой (радикальной оси) имеют одинаковую степень (различную для различных точек), составляет связку С. Совокупность всех С., относительно к-рых точки нек-рой плоскости (радикальной плоскости) имеют одинаковую степень (различную для разных точек), составляет пучок С.
С точки зрения дифференциальной геометрии, С. Sn -риманово пространство, имеющее постоянную (гауссову при n=2 и риманову при n>2) кривизну Все геодезич. линии С. замкнутьь и имеют постоянную длину
Все геодезич. линии С. замкнутьь и имеют постоянную длину  - это т. н. большие окружности, т. <е. пересечения с Sn двумерных плоскостей в Е п+1,проходящих через ее центр. Внешнегеометрич. свойства Sn:все нормали пересекаются в одной точке, кривизна любого нормального сечения одна и та же и не зависит от точки, в к-рой оно рассматривается, в частности имеет постоянную среднюю кривизну, причем полная средняя кривизна С. - наименьшая среди выпуклых поверхностей одинаковой площади, все точки С. омбилические.
- это т. н. большие окружности, т. <е. пересечения с Sn двумерных плоскостей в Е п+1,проходящих через ее центр. Внешнегеометрич. свойства Sn:все нормали пересекаются в одной точке, кривизна любого нормального сечения одна и та же и не зависит от точки, в к-рой оно рассматривается, в частности имеет постоянную среднюю кривизну, причем полная средняя кривизна С. - наименьшая среди выпуклых поверхностей одинаковой площади, все точки С. омбилические.
Нек-рые из таких свойств, принятые за основные, послужили отправной точкой для обобщения понятия С. Так, напр., аффинная сфера определяется тем, что все ее (аффинные) нормали пересекаются в одной точке; псевдосфера- поверхность в Е 3 постоянной гауссовой кривизны (но уже отрицательной); одна из интерпретаций орисферы (предельной сферы) - множество точек внутри S2. определяемое уравнением также второго порядка
На С. Sn дважды транзитивно действует ортогональная группа O(n+1) пространства Е п+1 (2-транзитивность означает, что для любых двух пар точек с равными расстояниями между ними существует вращение - элемент О(п+1), переводящее одну пару в другую); эта группа является полной группой изометрий Sn;наконец, С. есть однородное пространство: Sn=O(n+1)/O(n).
С точки зрения (дифференциальной) топологии, С. Sn - замкнутое дифференцируемое многообразие, разделяющее Е п+1 на две области и являющееся их общей границей; при этом ограниченная область, гомеоморфная Е п+1,-это (открытый) шар, так что С. можно определить как его границу.
Группы гомологии С. Sn,
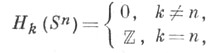
в частности Sn не стягивается в точку сама по себе, т. е. тождественное отображение Sn в себя cущественно.Группы гомотопий С. Sn,

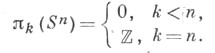
Напр.,
 при n>2. В общем случае - для любых kи п, k>n, группы
при n>2. В общем случае - для любых kи п, k>n, группы 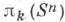 не вычислены ( см. Сфер гомотопические группы).
не вычислены ( см. Сфер гомотопические группы).
И здесь понятие С. получает обобщение. Напр., дикая сфера - топологич. С. (см. ниже) в Е п+1, не ограничивающая области, гомеоморфной Е п+1; Милнора сфера (экзотическая С.) - многообразие, гомеоморфное, но не диффеоморфное Sn.
Топологич. пространство, гомеоморфное С., наз. топологической сферой. Одним из основных здесь является вопрос об условиях того, что нек-рое пространство является топологич. сферой.Примеры.
а) Инвариантная топологич. характеристика С. Sn при n>2 не известна (1984). О случае п=1 см. Одномерное многообразие. Для того чтобы континуум был гомеоморфен С. S2, необходимо и достаточно, чтобы он был локально связан, содержал хотя бы одну простую замкнутую линию и чтобы всякая лежащая на нем такая линия разбивала его на две области, имеющие эту линию своей общей границей (теорема Уайлдера).б) Полное односвязное риманово пространство размерности
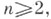 кривизна
кривизна 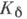 к-рого для всех касательных двумерных плоскостей
к-рого для всех касательных двумерных плоскостей  -ограничена с
-ограничена с 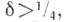 т. е.
т. е.  гомеоморфно Sn (теорема о сферe, см. Риманова геометрия).
гомеоморфно Sn (теорема о сферe, см. Риманова геометрия). в) Односвязное замкнутое гладкое многообразие, (целые) гомологии к-рого совпадают с гомологиями Sn, гомеоморфно Sn при
 (при п =3 - неизвестно (1984)). Если n = 5, 6, то оно также и гомеоморфно Sn (обобщенная гипотеза Пуанкаре), при n=3, 4 гипотеза остается (1984), при
(при п =3 - неизвестно (1984)). Если n = 5, 6, то оно также и гомеоморфно Sn (обобщенная гипотеза Пуанкаре), при n=3, 4 гипотеза остается (1984), при 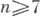 диффеоморфизм не имеет места.
диффеоморфизм не имеет места.
Совершенно аналогично определяется С. Sв метрич. пространстве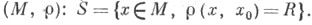
Однако это множество, вообще говоря, может быть устроено достаточно сложно (или может быть пустым).
В нормированном пространстве Кс нормой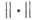 С. наз. множество
С. наз. множество  это, по существу, произвольная, вообще говоря, бесконечномерная выпуклая (гипер)поверхность, не всегда обладающая, напр., гладкостью, округлостью и т. п. полезными свойствами обычной С. Один из вариантов, применяющихся в топологии, - т. н. бесконечномерная сфера - строгий индуктивный предел
это, по существу, произвольная, вообще говоря, бесконечномерная выпуклая (гипер)поверхность, не всегда обладающая, напр., гладкостью, округлостью и т. п. полезными свойствами обычной С. Один из вариантов, применяющихся в топологии, - т. н. бесконечномерная сфера - строгий индуктивный предел 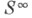 последовательности вложенных сфер:
последовательности вложенных сфер: 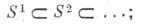
другое определение: где
где 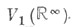 - бесконечномерное Штифеля многообразие. Для любого i оказывается, что
- бесконечномерное Штифеля многообразие. Для любого i оказывается, что 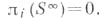
Приложения понятия С. чрезвычайно разнообразны. Напр., С. участвует в конструкциях новых пространств или дополнительных структур на них. Так, напр., проективное пространство можно интерпретировать как С. Sn с отождествленными диаметрально противоположными точками; С. с ручками и дырами используется в ручек теории;см. также Когомотопическая группа, Сферическое отображение.
можно интерпретировать как С. Sn с отождествленными диаметрально противоположными точками; С. с ручками и дырами используется в ручек теории;см. также Когомотопическая группа, Сферическое отображение. Лит.:[1] Розейфельд Б. А., Многомерные пространства, М., 1966; [2] его же. Неевклидовы пространства, М., 1969; [3]Лени П., Конкретные проблемы функционального анализа, пер. с франц., М, 19.67; [4] Введение в топологию, М., 1980; [5] Буземан Г., Геометрия геодезических, пер. с англ., М., 1962.
И. С. Шарадзе.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
