СПИНОРНОЕ ПРЕДСТАВЛЕНИЕ

простейшее точное линейное представление спинорной группы,Spin_n(Q) или определяющее его линейное представление объемлющей четной алгебры Клиффорда С ⁺=-С ⁺(Q). Если основное поле . алгебраически замкнуто, то алгебра С+ изоморфна полной матричной алгебре 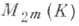(при n=2m+l) или алгебре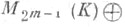 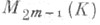(при п=2т). Тем самым определено линейное представление r алгебры С ⁺ в пространстве размерности 2 ^т над K, к-рое наз. спинорным. Ограничение наз. С. п. группы Spin_n(Q). С. п. при нечетном пнеприводимо, а при четном n распадается в прямую сумму двух неэквивалентных неприводимых представлений и 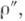к-рые наз. полуспинорными. Элементы пространства С. и. наз. спинорами, а полуспинорных - полуспинорами. С. п. спинорной группы Spin_n caмоконтрагредиентно при любом 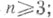полуспинорные представления 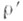и 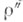спинорной группы Spin_2m caмоконтрагредиентны при четном . и контрагредиентны друг другу при нечетном т. С. п. группы Spin_n точно при любом 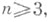полуспинорные представления группы Spin_2m точны при нечетном . и имеют ядро, состоящее из двух элементов, при четном m.
Если квадратичная форма Qзадана в пространство Vнад нек-рым подполем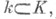 то С. п. не всегда определено над k. Однако, если индекс Витта квадратичной формы Qмаксимален, то есть равен [n/2] (в частности, если поле kалгебраически замкнуто), то спинорное и полуспинорные представления определены над k. В этом случае указанные представления могут быть описаны следующим образом (см. [1]). Пусть Lи М - непересекающиеся определенные над kмаксимальные вполне изотропные (относительно симметрической билинейной формы в V, ассоциированной с квадратичной формой Q) подпространства в V, C_L- подалгебра в алгебре Клиффорда C=C(Q), порожденная подпространством и - произведение твекторов, составляющих определенный над kбазис пространства М. Если n=2тчетно, то С. п. 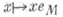реализуется в простом левом идеале Се _M и действует там с помощью левых сдвигов: Далее соответствие определяет изоморфизм векторных пространств 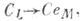что позволяет реализовать С. п. в пространстве C_L, естественно изоморфном внешней алгебре над пространством L. При этом полуспинорные представления и реализуются в инвариантных 2^m-1 -мерных подпространствах и
Если пнечетно, то пространство . можно включить в (n+1)-мерное векторное пространство над kиопределить в V₁ квадратичную форму Q₁, положив 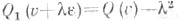при всех и При этом Q₁ -определенная над kневырожденная квадратичная форма максимального индекса Витта на четномерном векторном пространстве V₁. С. п. алгебры С ⁺(Q) (группы Spin_n (Q) получается путем ограничения любого пз полуспинорных представлений алгебры С ⁺(Q₁) (группы Spin_n+1(Q₁)) на подалгебру C⁺(Q) (соответственно подгруппу Spin_n(Q).
В случае, когда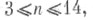 " a k- алгебраически замкнутое поле характеристики 0, решена задача классификации спиноров (см. [4], [8]. [9]), к-рая состоит в 1) описании всех орбит группы r (Spin_n) в пространстве спиноров, т. е. указании в каждой орбите нек-рого единственного представителя, 2) вычислении стабилизаторов группы Spin_n в каждом из этих представителей, 3) описании алгебры инвариантов линейной группы
Существование снинорных и полуспинорных представлений алгебр Ли групп Spin_n было открыто Э. Картаном (E. Cartau) в 1913, когда он классифицировал все неприводимые конечномерные представления простых алгебр Ли [6]. Впоследствии, в 1935 Р. Брауэр (R. Brauer) и Г. Вейль (Н. Wеyl) описали спинорные и полуспинорные представления в терминах алгебр Клиффорда [5]. П. Дирак (P. Dirac, [3]) обнаружил, что при помощи спиноров в квантовой механике описывается вращение электрона.

Лит.:[1] Бурбаки Н., Алгебра. Модули, кольца, формы, пер. cфранц., М., 1966; [2] Вейль Г., Классические группы, их инварианты и представления, пер. с нем., М., 1947; [3] Дирак П., Принципы квантовой механики, пер. с англ., 2 изд., М., 1079; [4] Попов В. Л., лТр. Моск. матем. об-ва