СПЕКТРАЛЬНОЕ РАЗЛОЖЕНИЕ

линейного оператора - представление оператора в виде интеграла по спектральной мере( спектральной функции). Для любого самосопряженного оператора Тв гильбертовом пространстве Нсуществует такая спектральная функция 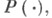что

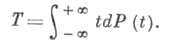
Это означает, что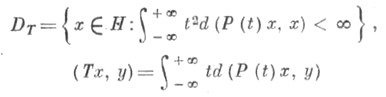

для любых 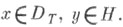Спектральная функция самосопряженного оператора Тможет быть вычислена через его резольвенту 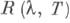по формуле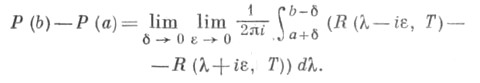

Из теоремы о С. р. самосопряженного оператора следует возможность реализации самосопряженных операторов операторами умножения и существование функционального исчисления на борелевских функциях.
Используя С. р. самосопряженного оператора и теорию расширений с выходом из пространства (см. [2]), можно получить интегральное представление симметрического оператора через обобщенную спектральную функцию. Аналогично строится интегральное представление изометрических операторов. При этом аналогия между С. р. самосопряженных и унитарных операторов, с одной стороны, и интегральными представлениями симметрических и изометрических - с другой, далеко не полная (отсутствие единственности обобщенных спектральных функций, отсутствие сильной сходимости интегралов, сравнительная узость функционального исчисления и т. п.).
Для любого ограниченного нормального оператора Т в гильбертовом пространстве Н существует такая счетно аддитивная в сильной операторной топологии самосопряженная спектральная мера на -алгебре борелевских подмножеств комплексной плоскости, что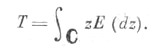

При этом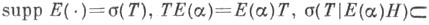 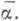Эта теорема допускает следующую удобную переформулировку: всякий ограниченный нормальный оператор унитарно эквивалентен оператору умножения на нек-рую существенно ограниченную функцию в пространстве 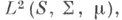причем мера 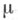может быть выбрана коночной, если пространство сепарабельно.
Из теоремы о С. р. следует существование функционального исчисления от нормального оператора, т. е. гомоморфизма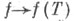 алгебры существенно ограниченных борелевских функций на 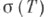в алгебру ограниченных операторов, удовлетворяющего условию id(T)=T и переводящего всякую ограниченную поточечно сходящуюся последовательность функций в сильно сходящуюся последовательность операторов. Образ этого гомоморфизма (т. е. множество всех функций от оператора Т)совпадает с множеством всех операторов, перестановочных с каждым оператором, перестановочным с Т. Поскольку из существования функционального исчисления, в свою очередь, следует теорема о С. р., этот результат можно считать одной из форм спектральной теоремы. Теорема о С. р. обобщается и на неограниченные нормальные операторы (см. [2]).
Спектральная мера в случае С. р. унитарного оператора - частного случая нормального оператора - может быть задана на единичной окружности. С. р. унитарного оператора Vиногда записывается в виде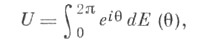

где 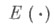- спектральная функция, сосредоточенная на отрезке 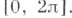Таким образом, С. р. дает возможность представить унитарный оператор в виде ехр iA, где А- самосопряженный оператор. Этот результат обобщает теорема Стоуна: всякая сильно непрерывная однопараметрическая группа унитарных операторов представляется в виде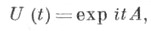

где А - самосопряженный (возможно, неограниченный) оператор.

Лит.:[1] Данфорд Н., Шварц Дж., Линейные операторы, пер. с англ., ч. 2 - Спектральная теория, М., 1966; [2] Ахиезер Н. И., Глазман И. М., Теория линейных операторов в гильбертовом пространстве, 2 изд., М., 1966.
В. С. Шулъман.