СИММЕТРИЗАЦИИ МЕТОД

(в теории функций) - один из методов решения экстремальных задач геометрич. теории функций. В основе метода лежит понятие симметризации замкнутых и открытых множеств п- мерного евклидова пространства. Впервые С. м. в теории функций был применен к изучению свойств трансфинитного диаметра (см. [1]), несколько позднее - к решению проблемы Карлемана - Миллу (см. [2]), а затем использовался достаточно широко (см. [3] - [6], [9]).

Использование С. м. в теории функций основано на монотонном характере изменения емкости конденсатора и внутреннего радиуса области при различных видах симметризации. Возможность применения С. м. при решении экстремальных задач геометрич. теории функций обусловливается определенной симметрией экстремальных отображений. Опираясь на свойство неубывания внутреннего радиуса области при ее симметризации относительно прямой или луча, с помощью теоремы об изменении внутреннего радиуса области при отображении ее посредством регулярной функции был получен следующий принцип симметризации (см. [4]): если функция w=f(z), f(0)=w₀, f'(0)=a₁, регулярна в круге 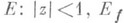- множество значений функции w=f(z). в 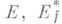- результат симметризации E_f относительно луча или прямой, проходящих через w=w₀,a 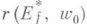- внутренний радиус области относительно точки w=w₀, то

(*)

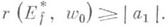Равенство в (*) имеет место тогда и только тогда, когда функция w=f(z)однолистна в E, а область 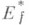совпадает с Е _f (при симметризации Штейнера) или получается из E_f в результате поворота вокруг w=w₀ (при симметризации Пойа). Аналогичный результат имеет место и для других видов симметризации, для к-рых справедливо свойство неубывания внутреннего радиуса. Дополнительное исследование обычно необходимо для выяснения условий достижимости в (*) равенства.

Имеются обобщения принципа симметризации на случай кольца и областей произвольной связности (см. [6]). Плодотворным оказывается сочетание С. м. с другими методами решения экстремальных задач геометрич. теории функций ( экстремальной метрики методом, теорией квадратичных дифференциалов и др.). Таким путем был получен ряд теорем покрытия и искажения для различных классов регулярных в данной области функций (однолистных, однолистных в среднем, слабо р-листных в круге или в кольце и др., см. [4] - (6]).

С. м. применяется также при изучении свойств пространственных квазиконформных отображений. Это обстоятельство особенно существенно в связи с ограниченными возможностями исследования таких отображений. С. м. позволяет находить среди двусвязных пространственных областей, обладающих определенными геомотрич. свойствами, область с наибольшим конформным модулем. Определение такой области в свою очередь позволяет установить нек-рое экстремальное свойство квазиконформного отображения. В частности, с помощью С. м. установлены нек-рые теоремы искажения для квазиконформных отображений в трехмерном евклидовом пространстве (см. [7], [8]).

Лит.:[1] F a b e r G., "Sitzungsber. Bayer. Akad. Wiss. Math.-naturwiss. Kl.", 1920, Bd 20, S. 49-64; [2] В e u r 1 i n g A..Etudes sur un probleme de majoration, Uppsala, 1933;[3] П o л и а Г., С е г ё Г., Изопериметрическис неравенства в математической физике, пер. [с англ.], М., 1962; [4] Х е й м а н В. К., Многолистные функции, пер. с англ., М., 1960; [5] Д ж е н к и н с Д ж., Однолистные функции и конформные отображения, пер. с англ., М., 1962; [6] Г о л у з и н Г. М., Геометрическая теория функций комплексного переменного, 2 изд., М., 1966; [7] Ш а б а т Б. В., "Докл. АН СССР", 1960, т. 132, № 5, с. 1045-48; [8] G e h r i n g F. W., "Trans. Amer. Math. Soc.", 1961, v. 101, № 3, p. 499-519; [9] B a e r n s t e i n A., "Acta math.", 1974, v. 133, p. 139-69.

И. П. Митюк.