ЛАГРАНЖЕВ ФОРМАЛИЗМ

ЛАГРАНЖЕВ ФОРМАЛИЗМ

- основанная на вариационном принципе формулировка механики и теории поля, в к-рой состояние системы задаётся обобщёнными координатами q_i и их производными по времени - обобщёнными скоростями (см. Вариационные принципы механики). Исходным для Л. ф. являются фун-дам. понятия действия S и его полной производной по времени, взятой вдоль траектории системы,- Лагранжа функции L(t); при этом . Для механич. системы с конечным числом степеней свободы (напр., для системы материальных точек) обычно принимают, что ф-ция Лагранжа зависит от q_i и :

(где q,- совокупность q ,). Существуют и обобщения Л. ф. на случаи, когда L зависит от высших производных q_i. Для систем с бесконечным числом степеней свободы - физ. полей - роль обобщённых координат играют значения компонент поля во всех пространств. точках x. Зависимость L от всех означает, что L является функционалом. Для физики наиб. интересны локальные функционалы, для к-рых вторая вариац. производная отлична от нуля лишь при . Тогда ф-ция Лагранжа может быть представлена в виде

,

а действие - в виде , где плотность ф-ции Лагранжа , называемая лагранжианом, зависит от полей (и, как правило, от их первых производных), взятых в одной и той же точке пространства-времени х, t.[Иногда термин "лагранжиан" используют и для самой ф-ции Лагранжа L(t), а наз. плотностью лагранжиана.]

В релятивистской теории и действие S, и лагранжиан являются скалярами относительно преобразований Пуанкаре группы. В четырёхмерных обозначениях переменные входят равноправно, и действие записывается как локальный функционал полей и их первых производных, заданных на нек-рой 4-области :

(принято сокращение ).

В механике и теории поля постулируется фундаментальный наименьшего действия принцип, утверждающий, что для реальных движений системы функционал S принимает экстрем. значение, т. е. его вариации . Ур-ния движения получаются из него по правилам вариац. исчисления как условия экстремума; они наз. Эйлера - Лагранжа уравнениями и имеют вид

где - "полная частная производная", учитывающая зависимость от х как явную, так и через поля , по повторяющемуся индексу предполагается суммирование. Т. о., задание формы лагранжиана полностью определяет ур-ния движения. [Для систем со связями =0 вариац. принцип применяется к модифициров. лагранжиану = , причём множители Лагранжа находятся интегрированием соответственно модифициров. ур-ний Эйлера - Лагранжа.]

При наличии в теории симметрии Л. ф. позволяет, помимо ур-ний движения, найти соответствующие сохранения законы с помощью Нётер теоремы. В силу этой теоремы из инвариантности действия относительно каждой однопараметрич. группы преобразований симметрии следует сохранение одной явно строящейся ф-ции координат и скоростей F(q, , t). В релятивистской теории аналогом момента времени t служит пространственноподобная поверхность , а аналогом сохранения во времени, dF/dt=0, является независимость от соответствующего функционала , полей и их производных:

Иными словами, каждой сохраняющейся величине F отвечает локальный четырёхмерный "ток" , удовлетворяющий дифференц. закону сохранения

В частности, всякое релятивистское описание должно быть инвариантно относительно трансляций и вращений в 4-пространстве (образующих 10-параметрич. группу Пуанкаре). Инвариантность S относительно преобразований группы Пуанкаре приводит к сохранению четырёх компонент энергии-импульса и шести компонент момента . Если взять поверхность а в виде x₀=t, то они выражаются ф-лами

через свои "токи" - тензоры энергии-импульса и момента , удовлетворяющие дифференциальным законам сохранения =0 и =0.

Эти тензоры находятся по заданному по формулам

где матрица описывает изменение многокомпонентного поля при бесконечно малом преобразовании Лорепца с параметром ,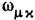

Если в теории имеются и др. группы симметрии, т. е. действие инвариантно относительно преобразований из этих групп, теорема Нётер даёт дополнит. сохраняющиеся величины (напр., заряды; см. Квантовая теория поля). В гамилътоновом формализме выясняется, что сохраняющиеся величины являются генераторами соответствующих преобразований симметрии. (Отметим, что в теориях, содержащих динамические симметрии, возникают дополнит. законы сохранения, к-рые не могут быть получены из теоремы Нётер.)

Т. о., лагранжиан полностью определяет теорию: Л. ф. даёт ур-ния движения и сохраняющиеся динамич. величины. Напротив, по заданной теории лагранжиан восстанавливается неоднозначно, напр. к нему всегда можно добавить 4-дивергенцию любой ф-ции, что не сказывается ни на ур-ниях движения, ни на сохраняющихся величинах.

Л. ф. играет важную эвристич. роль при построении матем. описания новой области явлений. Действительно, в соответствии с требованиями инвариантности относительно преобразований из группы Пуанкаре и др. групп симметрии может зависеть только от инвариантных комбинаций полей, к-рые нетрудно перечислить. Если ио соображениям простоты оставить в инварианты миним. степени по полям, получающиеся из Л. ф. ур-ния движения часто оказываются линейными. В этом случае они наз. уравнениями свободного поля. Так, для векторного поля с абелевой калибровочной группой (напр., эл.-магн. поля) все возможные лагранжианы эквивалентны выражению , где тензор поля = , - 4-потенциал, а ур-ния свободного поля имеют вид =0. В случае более сложной симметрии, напр. с неабелевой калибровочной группой, тензор поля

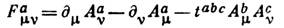
(где t^abc - структурные константы группы), а простейший лагранжиан . Уже простейшие нетривиальные ур-ния оказываются нелинейными по полю: , где - ко вариантная производная для. данной калибровочной группы.

Квантовая теория поля заимствует у классической весь Л. ф. с той лишь разницей, что полевые ф-ции являются теперь не с -числами, а, вообще говоря, некоммутирующими операторами. Поэтому операция варьирования, применяемая для вывода ур-ний движения и получения динамич. величин, требует доопределения [5, 6]; в ряде случаев (напр., в квантовой электродинамике) оно сводится к той или иной симметризации операторов.

Фундам. роль Л. ф. была вскрыта в лагранжевой форме квантовой динамики [Р. Фейнман (R. Feynman), 1948] - третьем, наряду с традиционными шрёдингеровым и гейзенберговым, способе её построения. На этом пути отщепление квантовой теории от классической связано с разными законами композиции вероятностей перехода между последоват. состояниями а, Ь, с,. . . динамич. системы. В то время как в классич. теории для вероятностей Р имеет место интуитивно очевидный мультипликативный закон композиции

(здесь "суммирование" производится по всем промежуточным конфигурациям Ь), в квантовой теории ему подчиняются не сами вероятности, а амплитуды А (такие, что Р _аЬ= . Матем. оформление этого утверждения эквивалентно введению функционального интеграла по значениям обобщённых координат в момент времени t на всех возможных траекториях системы. Все результаты обычной квантовой динамики получаются тогда из постулата, что фаза амплитуды есть классич. действие, измеренное в единицах :

Фейнмановский функциональный (континуальный) интеграл широко используется также в квантовой теории поля.

В квазиклассич. приближении, когда фазы велики, осн. вклад в континуальный интеграл даёт область, где фаза стационарна, т. е. =0 при вариации траекторий. Т. о., принцип наим. действия для классич. траекторий оказывается следствием квантовой динамики.

Лит.:1) Ландау Л. Д., Лифшиц Е. М., Механика, 4 изд., М., 1988; их же, Теория поля, 7 изд., М., 1988; 2) Арнольд В. И., Математические методы классической механики, 2 изд., М., 1979; 3) Медведев Б. В., Начала теоретической физики, М., 1977; 4) Боголюбов Н. Н., Ширков Д. В., Введение в теорию квантованных полей,

4 изд., М., 1984; 5) Березин Ф. А., Метод вторичного квантования, 2 изд., М., 1986; 6) Славнов А. А., Фаддеев Л. Д., Введение в квантовую теорию калибровочных полей, 2 изд., М., 1988. Б. В. Медведев, В. П. Павлов.

Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.