СЕПАРАБЕЛЬНОЕ РАСШИРЕНИЕ

п о л я - расширение K/kтакое, что для нек-рого натурального п поля Kи 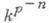линейно разделены над k(см. Линейно разделенные расширения). Расширение, не являющееся сепарабельным, наз. н е с е п а р а б е л ь н ы м.

В дальнейшем рассматриваются только алгебраич. расширения (о трансцендентных сепарабельных расширениям см. Трансцендентное расширение). Конечное расширение сепарабельно тогда и только тогда, когда отображение следа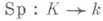является ненулевой функцией. Алгебраич. расширение сепарабельно, если любое конечное его подрасширение сепарабельно. В характеристике 0 все расширения сепарабельны.

С. р. образуют отмеченный класс расширений, т. е. в башне полей 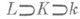расширение L/kсепарабельно тогда и только тогда, когда сепарабельны и L/Kи K/k. Если K₁/kи K₂/kсуть С. р., то и K₁K₂/kсепарабельно; для С. p. K/kи произвольного расширения L/kрасширение KL/Lснова сепарабельно. Расширение K/kсепарабельно тогда и только тогда, когда оно допускает погружение в некрое расширение Галуа L/k. При этом для конечного расширения K/kчисло различных k-изоморфизмов поля Kв Lсовпадает со степенью [K: k]. Любое конечное С. р. является простым.

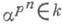Многочлен наз. с е п а р а б е л ь н ы м над k, если его неприводимые множители не имеют кратных корней. Алгебраич. элемент a наз. сепарабельным (над k),если он является корнем сепарабельного над kмногочлена. В противном случае a. наз. н е с е п а р а б е л ь н ы м. Элемент a. наз. ч и с т о н е с е п а р а б е л ь н ы м над k,если для нек-рого п. Неприводимый многочлен f(x)несепарабелен тогда и только тогда, когда производная f' (х) тождественно равна 0 (это возможно только в случае, когда kимеет характеристику ри f(х)=f₁(x^P).. Произвольный многочлен f(x)однозначно представим в виде , где g(x) - сепарабельный многочлен. Степень многочлена g(x). и число еназ. соответственно редуцированной степенью и индексом многочлена f(х).

Пусть L/k - произвольное алгебраич. расширение. Все элементы поля L, сепарабельные над k, образуют поле K,к-рое является максимальным С. р. поля k,содержащимся в L. Поле Kназ. сепарабельным замыканием поля kв L. Степень [K: k]наз. сепарабельной степенью расширения L/k, а степень [L: K] - несепарабельной степенью, или степенью несепарабельности. Несепарабельная степень равна нек-рой степени числа p=char k. Если K=k, то поле kназ, сепарабельно замкнутым в L. В этом случае расширение L/kназ. чисто несепарабельным. Расширение K/kчисто несепарабельно тогда и только тогда, когда

т. е. когда любой элемент поля Kчисто несепарабелен над k. Чисто Несепарабельные расширения поля kобразуют отмеченный класс расширений. Если расширение K/kодновременно сепарабельно и чисто несепарабельно, то K=k.

Лит. см. при ст. Расширение поля. Л. В. Кузьмин.