РАМСЕЯ ТЕОРЕМА

- название нескольких теорем в дискретной математике, сформулированных и доказанных Ф. Рамсеем [1].

Первую из этих теорем Ф. Рамсей сформулировал следующим образом. Пусть Г- бесконечный класс и m и r - положительные целые числа; и пусть все те подклассы Г, к-рые имеют r элементов или, иначе, все r-сочетания элементов Г, разделены любым способом на m, взаимно исключающих классов С _i, i=1, 2, . . ., m, так, что каждое r-сочетание является элементом одного и только одного класса С _i;тогда, предполагая справедливой аксиому выбора, класс Г должен содержать бесконечный подкласс D такой, что все r-сочетания членов D принадлежат одному и тому же классу С _i. К о н е ч н ы й а н а л о г этой Р. т., также установленный Ф. Рамсеем, можно сформулировать следующим образом.

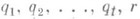Пусть S - множество, с. <одержащее Nэлементов, и Т - семейство всех подмножеств множества S, содержащих в точности r элементов из S. Пусть семейство Т разбито на t(непересекающихся) подсемейств T₁, Т ₂, . ..,T_t и пусть , r - целые числа, . Тогда существует такое минимальное число , зависящее только от и не зависящее от множества S, что если 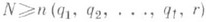, то для нек-рого i, i=l, 2, . . ., t, в Sсуществует подмножество А _i из 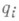элементов, все r-подмножества к-рого находятся в семействе T_i (доказательства этой теоремы содержатся также в [2], [3]).

Последнюю теорему можно пояснить примером, в к-ром вычисляется число п(3, 3, 2). Рассматриваются шесть точек на плоскости, связанных попарно дугами, каждая из к-рых окрашена либо в красный, либо в голубой цвета. Существуют три точки такие, что дуги, соединяющие их, окрашены в один и тот же цвет. Из пяти дуг, соединяющих нек-рую точку Р ₀ с пятью другими точками, три дуги одного цвета (напр., красного). Пусть это дуги 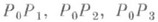. Если какая-нибудь из дуг 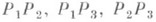красная, то она и две другие, соединяющие ее концы с точкой Р ₀, образуют красный треугольник, если же они все голубые, то сами образуют голубой треугольник. Это означает, что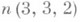 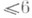. Однако пять точек на плоскости можно так попарно соединить красными и голубыми дугами, что при этом не найдется треугольника одного цвета. Для этого пусть дуги 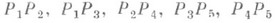будут красными, а остальные - голубыми. Это показывает, что n(3, 3, 2)>5. Таким образом, n(3, 3, 2) = 6.

Из Р. т. вытекает следующий результат: для данного натурального 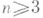существует целое число N=N(n).такое, что любые Nточек в плоскости, никакие три из к-рых не лежат на одной прямой, содержат пточек, образующих выпуклый n-угольник (см. [4]).

Лит.:[1] R a m s е у F. Р., "Ргос. London Math. Soc. Ser. 2", 1930, v. 30, p. 264-80; [2] P а й з е р Г.- Д ж., Комбинаторная математика, пер. с англ., М., 1966; [3] Х о л л М., Комбинаторика, пер. с англ., М., 1970; [4] Е г d о s P., S z e k e r e s G., "Compositio math.", 1935, v. 2, p. 463-70; [5] E r d o s P., R a d o R., "Bull. Amer . Math. Soc.", 1956, v. 62, p. 427-89.

М. П. Минеев.