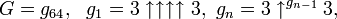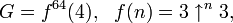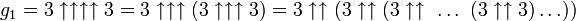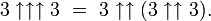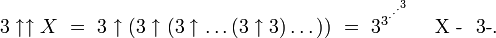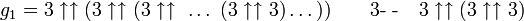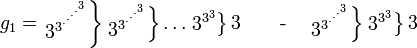Число Грехема

Число Грехема

Число Грехема, названное в честь Рональда Грехема, это большое число которое является верхней границей для решения некоторой проблемы в теории Рамсея.

Оно стало известно широкой публике после того, как Мартин Гарднер описал его в своей колонке «Математические игры» в журнале Scientific American в ноябре 1977, где было сказано «В неопубликованоом доказательстве, Грехем недавно установил … границу настолько большую, что ей принадлежит рекорд как наибольшему числу, когда-либо использовавшемуся в серьёзном математическом доказательстве».

В 1980 Книга рекордов Гиннесса повторила утверждения Гарднера, ещё больше подогрев интерес публики к этому числу. Число Грехема в невообразимое количество раз больше, чем другие хорошо известные большие числа, такие, как гугол, гуголплекс и даже больше, чем число Скьюза и число Мозера. На самом деле, вся наблюдаемая вселенная слишком мала, для того, что бы вместить в себя обыкновенную десятичную запись числа Грехема, предполагая, что запись каждой цифры занимает по меньщей мере объём Планка. Даже степенные башни вида 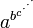$a ^{ b ^{ c ^{ \cdot ^{ \cdot ^{ \cdot}}}}}$ бесполезны для этой цели, хотя это число и может быть записано с использованием рекурсивных формул таких как стрельчатая нотация Кнута или эквивалентных, что и было сделано Грехемом. Последние 10 цифр числа Грехема это …2464195387.

В современных математических доказательствах иногда встречаются числа, ещё много большие, чем число Грехема, например в работе с конечной формой Фридмана в теореме Крускала.

Проблема Грехема

Число Грехема связано со следующей проблемой в области математики, известной как теория Рамсея:

Рассмотрим n-мерный гиперкуб и соединим все пары вершин для получения полного графа с 2ⁿ вершинами. Раскрасим каждое ядро этого графа либо в красный, либо в чёрный цвет. При каком наименьшем значении n каждая такая раскраска обязательно содержит раскрашенный в один цвет полный подграф с четырьмя вершинами, все из которых лежат в одной плоскости

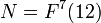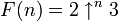Грехем и Ротщильд в 1971 доказали, что это проблема имеет решение, N*, и показали что 6 ≤ N* ≤ N, где N — конкретное, точно определённое, очень большое число. (На языке стрельчатой нотации Кнута оно может быть записано как $N = F^7(12) \,\!$, где $F(n) = 2\uparrow^{n} 3 \,\!$). Нижняя граница 6 ,была впоследствии улучшена Экзу [2003], который показал, что решение должно быть как минимум 11 и продемонстрировал экспериментальные свидетельства в пользу того, что оно, по меньшей мере 12. Таким образом, наиболее известные границы для N* на сегодня 11 ≤ N* ≤ N.

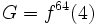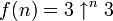Предметом настоящей статьи является верхняя граница G, которая много слабее (то есть больше) чем N; а именно $G = f^{64}(4) \,\!$, где $f(n) = 3 \uparrow^n 3 \,\!$. Именно эта граница, описанная в неопубликованной работе Грехема, и была описана (и названа числом Грехема) Мартином Гарднером.

Определение числа Грехема

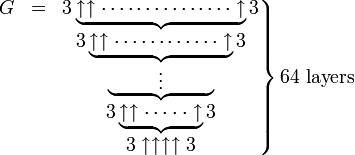
Используя стрельчатую нотацию Кнута, число Грехема G может быть записано как

$\left. \begin{matrix} G &=&3\underbrace{\uparrow \uparrow \cdots\cdots\cdots\cdots\cdots \uparrow}3 \\ & &3\underbrace{\uparrow \uparrow \cdots\cdots\cdots\cdots \uparrow}3 \\ & &\underbrace{\qquad\;\; \vdots \qquad\;\;} \\ & &3\underbrace{\uparrow \uparrow \cdots\cdot\cdot \uparrow}3 \\ & &3\uparrow \uparrow \uparrow \uparrow3 \end{matrix} \right \} \text{64 layers}$

где количество стрелок в каждом слое, начиная с верхнего, определяется числом в следующем слое, то есть

$G = g_{64},\text{ где }g_1=3\uparrow\uparrow\uparrow\uparrow 3,\ g_n = 3\uparrow^{g_{n-1}}3,$

и где верхний индекс у стрелки показывает общее количество стрелок. Другими словами, G вычисляется в 64 шага: на первом шаге мы вычисляем g₁ с четырьмя стрелочками между тройками, на втором — g₂ с g₁ стрелочек между тройками, на третьем — g₃ с g₂ стрелок между тройками и так далее, в конце мы вычисляем G = g₆₄ с g₆₃ стрелочек между тройками.

Это может быть записано как

$G = f^{64}(4),\text{ где }f(n) = 3 \uparrow^n 3,$

где верхний индекс у f означает итерации функций. Функция f является частным случаем гипероператоров, f(n) = hyper(3,n + 2,3), и может быть так же записана при помощи нотации цепных стрелок Конуэя как 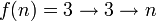$f(n) = 3 \rightarrow 3 \rightarrow n$. Последняя запись так же позволяет записать следующие граничные значения для G: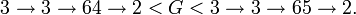

$3\rightarrow 3\rightarrow 64\rightarrow 2 < G < 3\rightarrow 3\rightarrow 65\rightarrow 2.\,$

Массштаб числа Грехема

Для того, что бы осознать невероятный размер числа Грехема, полезно попробовать представить через возведение в степень хотя бы первый член (g₁) стремительно растущей 64-членной последовательности. На языке тетратионов $\uparrow\uparrow$) означает:

$g_1 = 3 \uparrow \uparrow \uparrow \uparrow 3 = 3 \uparrow \uparrow \uparrow (3 \uparrow \uparrow \uparrow 3) = 3 \uparrow\uparrow (3 \uparrow\uparrow (3 \uparrow\uparrow \ \dots \ (3 \uparrow\uparrow 3) \dots ))$

где число троек в выражении справа

$3 \uparrow \uparrow \uparrow 3 \ = \ 3 \uparrow \uparrow (3 \uparrow \uparrow 3).$

Теперь каждый тетратион ($\uparrow\uparrow$) по определению разворачивается в «степенную башню» как

$3 \uparrow\uparrow X \ = \ 3 \uparrow (3 \uparrow (3 \uparrow \dots (3 \uparrow 3) \dots )) \ = \ 3^{3^{\cdot^{\cdot^{\cdot^{3}}}}} \quad \text{где X - количество 3-ек}.$

Таким образом,

$g_1 = 3 \uparrow\uparrow (3 \uparrow\uparrow (3 \uparrow\uparrow \ \dots \ (3 \uparrow\uparrow 3) \dots )) \quad \text{ где количество 3-ек -} \quad 3 \uparrow \uparrow (3 \uparrow \uparrow 3)$

записанное на языке степеней

$g_1 = \left. \begin{matrix}3^{3^{\cdot^{\cdot^{\cdot^{\cdot^{3}}}}}}\end{matrix} \right \} \left. \begin{matrix}3^{3^{\cdot^{\cdot^{\cdot^{3}}}}}\end{matrix} \right \} \dots \left. \begin{matrix}3^{3^3}\end{matrix} \right \} 3 \quad \text{где количество башен -} \quad \left. \begin{matrix}3^{3^{\cdot^{\cdot^{\cdot^{3}}}}}\end{matrix} \right \} \left. \begin{matrix}3^{3^3}\end{matrix} \right \} 3$

и где количество троек в каждой башне, начиная слева, указывается предыдущей башней.

Другими словами, g₁ выисляется путём выисления количества бащен, n = 3³³^…³ (где число троек — 3³³ = 7625597484987), и затем вычисляя n бащен в следующем порядке:

      1ая бащня:  3

      2ая башня:  3^3^3 (number of 3s is 3) = 7625597484987

      3ья башня:  3^3^3^3...^3 (number of 3s is 7625597484987) = ...

      .
      .
      .

 g1 = nтая башня:  3^3^3^3^3^3^3^...^3 (количество 3-ек задаётся результатом выисления n-1ой башни)

Масштаб первого члена, g₁, настолько велик, что его практически невозможно осознать, хотя запись выше относительно проста для понимания. Хотя n это всего лишь количество башен в этой формуле для g₁, уже это число много больше количества объёмов Планка которые содержатся в наблюдаемой вселенной (примерно 10^185). А после первого члена нас ожидает ещё 63 члена стремительно растущей последовательности!

См. также

• теорема Крускала
• функция Аккермана

Ссылки

• Graham, R. L.; Rothschild, B. L. (1971). «Ramsey's Theorem for n-Parameter Sets». Transactions of the American Mathematical Society 159: 257-292. DOI:10.2307/1996010. The explicit formula for N appears on p. 290.
• Graham, R. L.; Rothschild, B.L. (1978). «Ramsey Theory», Studies in Combinatorics, Rota, G.-G., ed., Mathematical Association of America, 17:80-99. On p. 90, in stating «the best available estimate» for the solution, the explicit formula for N is repeated from the 1971 paper.
• Gardner, Martin (November 1977). «Mathematical Games». Scientific American 237: 18-28.; reprinted (revised 2001) in the following book:
• Martin Gardner The Colossal Book of Mathematics: Classic Puzzles, Paradoxes, and Problems. — New York, NY: Norton, 2001. — ISBN 0393020231
• Martin Gardner Penrose Tiles to Trapdoor Ciphers. — Washington, D.C.: Mathematical Association of America, 1989. — ISBN 0-88385-521-6
• Exoo, Geoffrey (2003). «A Euclidean Ramsey Problem». Discrete Computational Geometry 29: 223-227. DOI:10.1007/s00454-002-0780-5.

Внешние ссылки

• «A Ramsey Problem on Hypercubes» by Geoff Exoo
• Mathworld article on Graham’s number
• How to calculate Graham’s number
• Numeropedia — the Special Encyclopedia of Numbers