ВЫБОРА ТЕОРЕМЫ

- группа теорем комбинаторики, связанных с выбором элементов из множества, тем или иным способом соответствующих семейству подмножеств этого множества. В. т. обычно используются в качестве теорем существования при решении различных комбинаторных задач. Ниже формулируются век-рые наиболее важные из В. т. и указываются примеры их применения.

1) Пусть - некоторое семейство подмножеств данного множества .

Набор различных элементов множества Тназ. системой различных представителей (с. р. п.) семейства S, если 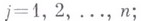элемент наз. представителем множества . Напр., если и Sсостоит из то есть с. р. п. для- S, где элемент 5 представляет множество , элемент 2 - множество и т. д. Если же Sсоставить из множеств то для Sне существует с. р. п., так как вместе содержат только три элемента.

Теорема о системе различных представителей. Семейство тогда и только тогда имеет с. р. п., когда объединение каждых kмножеств из Sсодержит по крайней мере kразличных элементов, k=1, 2, ..., п.

Эта теорема доказана Ф. Холлом [3] (см. также [1], [2]). С ее помощью доказывается теорема о системе общих представителей, также относящаяся к В. т. Пусть

суть два разбиения множества Т, в к-рых ни одно из составляющих не пусто. Множество наз. системой общих представителей (с. о. п.) разбиений (1) и (2), если Rявляется с. р. п. как для семейства 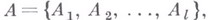так и для семейства Напр., если и

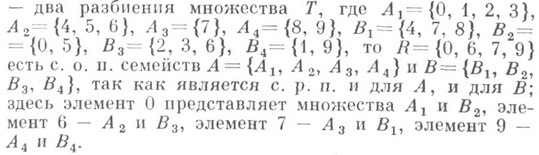
Теорема о системе общих представителей. Разбиения (1) и (2) имеют с. о. п. тогда и только тогда, когда объединение каждых kмножеств из семейства Асодержит не более kмножеств из семейства (см. [1], [2]).

2) Пусть задана прямоугольная матрица. Линией в матрице наз. как строку, так и столбец этой матрицы.

Теорема Кен и г а. Если элементы прямоугольной матрицы - нули и единицы, то минимальное число линий, содержащих все единицы, равно максимальному числу единиц, к-рые могут быть выбраны таким образом, чтобы среди них не нашлось двух, расположенных на одной и той же линии.

Эта теорема сформулирована и доказана Д. Кёнигом ([4], с. 240; см. также [1], [2]). Она эквивалентна теореме Холла о с. р. п. Используется, напр., при доказательстве того, что нек-рые матрицы являются линейными комбинациями перестановочных матриц (перестановочная матрица - такая прямоугольная матрица Рразмера , состоящая из нулей и единиц, что , где Р' - транспонированная матрица Р, а I - единичная матрица порядка т; напр., перестановочная квадратная матрица порядка mсостоит из mединиц, расположенных так, что никакие две из них не лежат на одной линии). Иными словами, если дана матрица Аразмера , , элементами к-рой являются неотрицательные действительные числа, причем сумма элементов каждой строки в Аравна т' , а сумма элементов каждого столбца равна п', то где каждое P_i есть перестановочная матрица, а коэффициенты с _i - неотрицательные действительные числа (ем. [1], [2]). В частности, если квадратная матрица Апорядка п, состоящая из нулей и единиц, такова, что суммы элементов по любой строке или любому столбцу равны целому положительному числу k, то

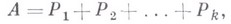
где все - перестановочные матрицы порядка п.3) Пусть Т - конечное множество и - множество всех его подмножеств, содержащих точно г элементов. Пусть

- произвольное упорядоченное разбиение Р _r (Т).(на lсоставляющих А ₁ , А ₂ , . . ., A_l ). Пусть q₁,q₂,...,q_l - такие целые числа, что

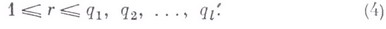
Если существует такое подмножество, содержащее q_i элементов множества Т, что все его подмножества, содержащие точно rэлементов, содержатся именно в A_i , то оно наз. (q_i, А _i )-подмножеством множества Т.

Теорема Рамсе я. Пусть заданы целые числа удовлетворяющие условию (4). Тогда существует натуральное число обладающее тем свойством, что для любого Целого числа справедливо следующее: если даны множество Т, состоящее из пэлементов, и произвольное упорядоченное разбиение (3) множества на lсоставляющих то Тсодержит - подмножество для некоторого

Эта теорема доказана Ф. Рамсеем ([5]; см. также [1], [2]). Примером приложения теоремы Рамсея служит следующий результат (см. [6], [1], [2]): для любого заданного целого числа существует такое целое число

, что среди точек плоскости, расположенных так, что никакие три из них не лежат на одной прямой, найдутся mточек, образующих выпуклый m-угольник.

Лит.: [1] Холл М., Комбинаторный анализ, пер. с англ., М., 1963; [2] Райзер Г. Д ж., Комбинаторная математика, пер. с англ., М., 1966; [3] Hall Ph., "J. London Math. Soc.", 1935, v. 10, p. 26-30; [4] Konig D., Theorie der Endlichen und Unendiichen Graphen, Leipzig, 1936; [5] Ramsеу F. P., "Proc. London Math. Soc.", (2), 1930, v. 30, p. 264-286; [6] Erdos P., Szekeres G., "Compositio Mathematica", 1935, v. 2, № 3, p. 463-70. M. П. Минеев.