- РАЗНОСТНЫЙ ОПЕРАТОР
оператор, действующий в пространстве сеточных функций. Р. о. возникают при аппроксимации дифференциальной задачи разностной и являются предметом изучения разностных схем теории. Разностную схему можно рассматривать как операторное уравнение с операторами, действующими в нек-ром функциональном пространстве, а именно в пространстве сеточных функций. Под пространством сеточных функций понимается множество функций, определенных в точках заданной сетки и образующих конечномерное векторное пространство. Пространства сеточных функций обычно возникают при аппроксимации того или иного пространства функций непрерывного аргумента.
П р и м е р 1. Пусть С[0, 1] - пространство непрерывных функций, заданных на отрезке
с нормой 
Вводится сетка
и рассматривается множество С h, [0, 1] функций
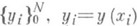, заданных на сетке wh. Множество С h[0, 1] образует (N+1)-мерное векторное пространство относительно покоординатного сложения и умножения на число. Норма в Ch[0, 1]
согласована с нормой в С[0, 1] в том смысле, что для любой функции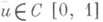 
определен вектор
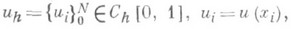
и существует
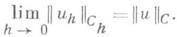
Любой линейный Р. о.
как оператор, действующий в конечномерном пространстве, может быть представлен матрицей. Характерными свойствами матриц, порождаемых разностными операторами, являются их большой размер и относительно большое число нулевых элементов.
В общем случае конструкция пространств сеточных функций и Р. о. может быть весьма сложной. Наиболее изучены свойства Р. о., действующих в пространствах с гильбертовой метрикой. В этом случае наибольший интерес представляют такие свойства Р. о., как самосопряженность и положительность. В основе математич. аппарата, позволяющего исследовать свойства Р. о., лежат разностные аналоги формул дифференцирования произведения и интегрирования по частям.
П р и м е р 2. Пусть задано множество действительных функций на сетке wh. Вводятся обозначения:
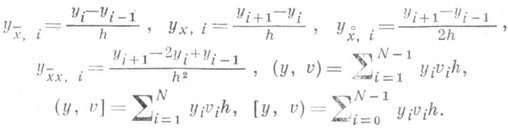
Справедливы следующие формулы:
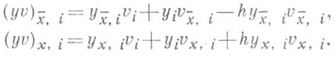
Имеет место также формула суммирования по частям
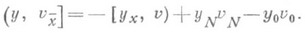
Из последней формулы следует, в частности, самосопряженность и положительность оператора второй разностной производной
на множестве функций, заданных на сетке wh и обращающихся в нуль на границе i=0, i=N.
Многочисленные исследования посвящены изучению свойств разностных аппроксимаций дифференциальных операторов эллиптич. типа (см. [1]-[4]). Для построения соответствующих Р. о. используются такие эффективные методы, как метод баланса, конечных элементов, вариационные и проекционные методы. Найденные разностные аппроксимации хорошо моделируют основные свойства исходных операторов, такие, напр., как эллиптичность, выполнение принципа максимума и др. Построены также Р. о., аппроксимирующие эллиптические дифференциальные операторы в областях сложной формы при различных типах краевых условий и в случае нерегулярных сеток (см. [5]).
Свойства стационарных Р. о. используются для изучения устойчивости нестационарных разностных задач и для построения итерационных методов. При этом теория итерационных методов может быть изложена как один из разделов общей теории устойчивости разностных схем (см. [6], [7]).
В связи с построением экономичных разностных схем для многомерных задач математич. физики исследованы факторизованные Р. о., то есть многомерные Р. о., представимые в виде произведения одномерных Р. о. (см. [1]). Изучались и нелинейные Р. о. (см. [8]).
Лит.:[1] С а м а р с к и й А. А., Теория разностных схем, М., 1977; [2] С а м а р с к и й А. А., А н д р е е в В. Б., Разностные методы для эллиптических уравнений, М., 1976; [3] К о р н е е в В. Г., Схемы метода конечных элементов высоких порядков точности, Л., 1977; [4] О б э н Ж.-П., Приближенное решение эллиптических краевых задач, пер. с англ., М., 1977; [5] С а м а р с к и й А. А., Ф р я з и н о в И. В., "Успехи матем. наук", 1976, т. 31, в. 6, с. 167-97; [6] С а м а р с к и й А. А., Г у л и н А. В., Устойчивость разностных схем, М., 1973; [7] С а м а р с к и й А. А., Н и к о л а е в Е. С., Методы решения сеточных уравнений, М., 1978; [8] К а р ч е в с к и й М. М., Л я ш к о A. Д., "Изв. вузов. Математика", 1972, № 11, с. 23-31; 1973, № 3, с. 44 - 52. А. В. Гулин, А. А. Самарский.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
