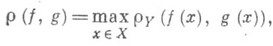РАВНОСТЕПЕННАЯ НЕПРЕРЫВНОСТЬ
- РАВНОСТЕПЕННАЯ НЕПРЕРЫВНОСТЬ
множества функций- понятие, тесно связанное с понятием компактности множества непрерывных функций. Пусть X, Y - компактные метрич. пространства и С(X, Y) - множество непрерывных отображений Xв Y. Множество  наз. равностепенно непрерывным, если для любого
наз. равностепенно непрерывным, если для любого 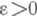 существует такое
существует такое 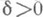 , что из
, что из 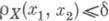 вытекает
вытекает 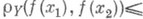
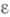 для всех
для всех 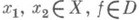 . Р. <н. Dэквивалентна относительной компактности Dв С( Х, Y), наделенном метрикой
. Р. <н. Dэквивалентна относительной компактности Dв С( Х, Y), наделенном метрикой
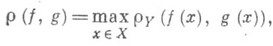
что составляет содержание теоремы Арцела - А с к о л и. Понятие Р. н. переносится на топологич. пространства.
Лит.:[1] Колмогоров А. Н., Ф о м и н С. В., Элементы теории функций и функционального анализа, 5 изд., М., 1981; [2] Э д в а р д с Р., Функциональный анализ, пер. с англ., М., 1969. Е. М. Семенов.
Математическая энциклопедия. — М.: Советская энциклопедия.
И. М. Виноградов.
1977—1985.
Смотреть что такое "РАВНОСТЕПЕННАЯ НЕПРЕРЫВНОСТЬ" в других словарях:
Равностепенная непрерывность — Не следует путать с Равномерная непрерывность. Равностепенная непрерывность свойство семейства непрерывных функций. Содержание 1 Определение 2 Свойства 3 … Википедия
Равностепенная непрерывность — важное свойство некоторых семейств функций. Семейство функций называется равностепенно непрерывным на данном отрезке [а, b], если для всякого числа ε > 0 найдётся такое δ > 0, что |f (x2) f (x1)| < ε для любых x1 и x2 из [а, b] для… … Большая советская энциклопедия
Равномерная непрерывность — в математическом и функциональном анализе это свойство функции быть одинаково непрерывной во всех точках области определения. Содержание 1 Определения 1.1 Равномерная непрерывность числовых функций … Википедия
Теорема Асколи — Теорема Арцела утверждение, которое представляет собой критерий предкомпактности множества в полном метрическом пространстве в том специальном случае, когда рассматриваемое пространство пространство непрерывных функций на отрезке… … Википедия
Теорема Асколи — Арцела — Теорема Арцела утверждение, которое представляет собой критерий предкомпактности множества в полном метрическом пространстве в том специальном случае, когда рассматриваемое пространство пространство непрерывных функций на отрезке… … Википедия
МЕРА — в топологическом векторном пространстве термин, употребляемый применительно к мере, заданной в топологическом векторном пространстве, когда хотят подчеркнуть те свойства этой меры, к рые связаны с линейной и топологич. структурой этого… … Математическая энциклопедия
Компактность — (математическое) важное свойство множеств; множество называется компактным, если каждая бесконечная последовательность его элементов (точек) имеет хотя бы одну предельную точку (См. Предельная точка). От К. по отношению к объемлющему… … Большая советская энциклопедия
УСЛОВНАЯ УСТОЙЧИВОСТЬ — точки относительно семейства отображений равностепенная непрерывность в этой точке семейства сужений отображений f t на нек рое вложенное в Емногообразие V;здесь G+ множество неотрицательных чисел: действительных или целых У. у. точки… … Математическая энциклопедия
УСТОЙЧИВОСТЬ ПО ЛЯПУНОВУ — точки относительно семейства отображений нек рого пространства Е равностепенная непрерывность этого семейства отображений в этой точке (здесь G+ множество неотрицательных чисел: действительных или целых У. по Л. точки относительно семейства… … Математическая энциклопедия
Равномерно непрерывная функция — Равномерная непрерывность в математическом и функциональном анализе это свойство функции быть одинаково непрерывной во всех точках области определения. Содержание 1 Определения 2 Замечание 3 Свойства 4 См. также … Википедия
 наз. равностепенно непрерывным, если для любого
наз. равностепенно непрерывным, если для любого 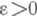 существует такое
существует такое 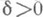 , что из
, что из 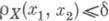 вытекает
вытекает 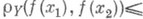
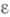 для всех
для всех 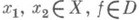 . Р. <н. Dэквивалентна относительной компактности Dв С( Х, Y), наделенном метрикой
. Р. <н. Dэквивалентна относительной компактности Dв С( Х, Y), наделенном метрикой