- РАВНОСХОДЯЩИЕСЯ РЯДЫ
такие сходящиеся или расходящиеся числовые ряды
а п и 
, разность к-рых является сходящимся рядом с суммой, равной нулю: 
. Если же их разность является лишь сходящимся рядом, то исходные ряды наз. равносходящимися в широком смысле.
Если а п -а п (х)и b п=b п (х).- функции, напр. а n:
, b п: 
, где X - произвольное множество, а 
- множество действительных чисел, то ряды
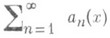и 
наз. равномерно равносходящимися (равномерно равносходящимися в широком смысле) на множестве X, если их разность есть ряд, к-рый равномерно сходится на Xи его сумма равна нулю (соответственно просто равномерно сходится на X).
Пример. Если две интегрируемые на отрезке [-p, p] функции равны на интервале
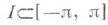, то их ряды Фурье - равномерно равносходящиеся на каждом интервале I*, внутреннем к интервалу I, а сопряженные ряды Фурье - равномерно равносходящиеся на I* в широком смысле. Л. Д. Кудрявцев.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
