ПСЕВДОЕВКЛИДОВО ПРОСТРАНСТВО

действительное аффинное пространство, в к-ром каждым двум векторам a и b поставлено в соответствие определенное число, называемое скалярным произведением ( а, b).

1) Скалярное произведение коммутативно: ( а, b) =(b, а).

2) скалярное произведение дистрибутивно относительно сложения векторов: ( а(b + с)) = ( а, b) +( а, с).

3) числовой множитель можно вынести за знак скалярного произведения: (ka, b) = k(a, b).

4) существуют такие пвекторов а_i, что

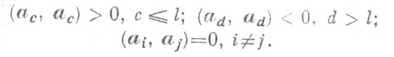
Число пназ. размерностью П. п., l - индексом, пара чисел (l, р), р=п-l, -сигнатурой. П. п. обозначается Е (l,р) (или ^l Е _п). Пространство Е (1,3₎ наз. Минковского пространством. В пространстве E(l,p) во всякой системе пвекторов b_i, для к-рых 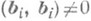и (b_i, b_j)=0 при 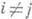, число векторов b_i, для к-рых (b_i, b_i)>0, равно l, а число векторов b_i, для к-рых (b_i, b_i)<0, равно п-l (закон инерции квадратичной форм ы).

Модуль | а| вектора аП. п. может быть определен как неотрицательный корень 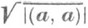. Векторы, скалярные квадраты к-рых равны 1 и -1, наз. соответственно единичными и мнимоединичными векторами. Векторы x, для к-рых (x, x)=0, обладают нулевым модулем и наз. изотропными векторами; направления изотропных векторов - изотропными направлениями.

В П. п. имеются три вида прямых: евклидовы, направляющий вектор к-рых имеет положительный скалярный квадрат (( а, а)>0), псевдоевклидовы ( а, а)<0) и изотропные ((a, а)=0). Совокупность всех изотропных прямых, проходящих через нек-рую точку, наз. изотропным конусом.

В П. п. имеется несколько видов плоскостей: евклидовы плоскости Е ², псевдоевклидовы плоскости E(1;1) и плоскости, содержащие изотропные векторы,- т. н. полуевклидовы плоскости сигнатуры (0,1) и (1,0) и дефекта 1 (см. Полуевклидово пространство).и изотропные плоскости, все векторы к-рых изотропны.

За расстояние между точками А(x )и В(x) принимается модуль вектора 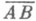, и оно может быть вычислено следующим образом:

П. п. не является метрич. пространством, т. к. в нем не выполняется неравенство треугольника. Если векторы а и b принадлежат евклидовой плоскости (или псевдоевклидовой плоскости индекса 0), то для них выполняется неравенство треугольника, а если они принадлежат псевдоевклидовой плоскости индекса 1, то для них выполняется т. н. обратное неравенство треугольника:

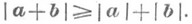
В П. п. имеются три вида сфер: сферы с положительным квадратом радиуса: (x, x)=r², сферы с отрицательным квадратом радиуса: ( х, x)=- s² и сферы нулевого радиуса: (x, x)=0, совпадающие с изотропным конусом.

Движения П. <п. являются аффинными преобразованиями я могут быть записаны в виде x' = Ux +a.

Оператор Uудовлетворяет условию |Ux|=|x|, т. <е. сохраняет расстояние между точками. Движения П. п. образуют группу по умножению; она зависит от n(n+1)/2 независимых параметров. Движения П. п. наз. движениями 1-го или 2-го рода, если они являются аффинными преобразованиями соответствующего рода.

Антидвижением П. п. называют геометрич. преобразование, при к-ром всякий вектор апереходит в вектор а' такой, что ( а, а)=-( а', а').

В П. п. можно ввести основные операции векторной и тензорной алгебры. Основные дифференциально-геометрич. понятия строятся в соответствии с правилами геометрии псевдоримановых пространств. Метрич. тензор П. п. имеет вид (в галилеевой системе координат)

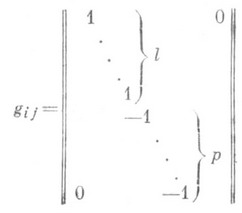
П. п. является плоским, т. е. его Римана тензор равен нулю. Если тензор Римана псевдориманова пространства равен нулю тождественно, то оно является л о-кально псевдоевклидовым пространством.

Подмногообразия П. п. могут нести различные метрики: положительно или отрицательно определенную риманову метрику, псевдориманову метрику и вырожденную метрику (см. Индефинитная метрика). Так, напр., сферы П. п. несут (вообще говоря, индефинитную) метрику постоянной кривизны. В E(1, n-1) сфера с положительным квадратом радиуса является ( п-1)-мерным пространством, изометричным пространству Лобачевского.

П. п. E(l, _p)(l+р=п).и евклидово пространство Е ⁿ можно рассматривать как подпространства комплексного пространства с формой 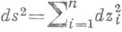. Если x^j - координаты П. п., y^j - действительного евклидова пространства, z^j - комплексного евклидова пространства, то уравнения подпространств имеют вид

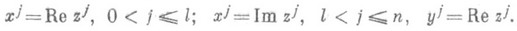
Метрику П. п. можно формально получить из метрики евклидова пространства заменой

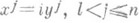
Лит.:[1] Ефимов Н. В., Розендорн Э. Р., Линейная алгебра и многомерная геометрия, М., 1970; [2] Розен-фельд В. А., Многомерные пространства, М., 1966; [3] Ландау Л. Д., Лифшиц Е. М., Теория поля, 6 изд., М., 1973.