- ПРИБЛИЖЕНИЕ ФУНКЦИЙ
случай многих действительных переменных - случай, когда приближаемая функция f зависит от двух и большего
 числа переменных: (см. Приближение функций). По сравнению с одномерным случаем исследование вопросов приближения функций т(т
числа переменных: (см. Приближение функций). По сравнению с одномерным случаем исследование вопросов приближения функций т(т  2) переменных значительно усложняется ввиду появления принципиально новых обстоятельств, связанных с многомерностью. Прежде всего это касается области, на к-рой осуществляется приближение. Просто связный компакт (в одномерном случае - отрезок) в
2) переменных значительно усложняется ввиду появления принципиально новых обстоятельств, связанных с многомерностью. Прежде всего это касается области, на к-рой осуществляется приближение. Просто связный компакт (в одномерном случае - отрезок) в  (даже на плоскости) может иметь самую разнообразную конфигурацию, и возникает необходимость классифицировать области в зависимости, напр., от гладкостных свойств их границ. Сложности появляются и при описании дифференциально-разностных свойств функций тпеременных. Эти свойства могут быть, вообще говоря, различными по разным направлениям, их характеризация должна учитывать как геометрию области определения, так и поведение функции при подходе к границе, так что большое значение приобретает изучение граничных свойств функций. Если пытаться упростить решение аппроксимационной задачи переходом к области более простой структуры, то возникает проблема возможности продолжения функции f из области
(даже на плоскости) может иметь самую разнообразную конфигурацию, и возникает необходимость классифицировать области в зависимости, напр., от гладкостных свойств их границ. Сложности появляются и при описании дифференциально-разностных свойств функций тпеременных. Эти свойства могут быть, вообще говоря, различными по разным направлениям, их характеризация должна учитывать как геометрию области определения, так и поведение функции при подходе к границе, так что большое значение приобретает изучение граничных свойств функций. Если пытаться упростить решение аппроксимационной задачи переходом к области более простой структуры, то возникает проблема возможности продолжения функции f из области  в нек-рую содержащую Qканонич. область Q1 (напр., в параллелепипед или на все пространство
в нек-рую содержащую Qканонич. область Q1 (напр., в параллелепипед или на все пространство  ) с сохранением тех или иных гладкостных свойств (см. Продолжения теоремы). Этот круг вопросов тесно связан с вложения теоремами, а также с проблемами, возникающими при решении краевых задач математич. физики.
) с сохранением тех или иных гладкостных свойств (см. Продолжения теоремы). Этот круг вопросов тесно связан с вложения теоремами, а также с проблемами, возникающими при решении краевых задач математич. физики.
Увеличение числа независимых переменных, естественно, усложняет и аппарат приближения, ибо увеличивается его размерность при том же, напр., порядке полиномов. Алгебраич. многочлен степени n1, . . ., п т соответственно по переменным t1,. . ., tm имеет вид
 (1)
(1)
(
 - действительные коэффициенты, суммирование ведется по kv , v= 1,. . ., т, от 0 до nv), так что, напр., подпространство многочленов степени 3 по каждому из тпеременных имеет размерность 4m. Иногда фиксируется суммарная степень многочлена n, тогда суммирование в (1) распространено на индексы, удовлетворяющие неравенству
- действительные коэффициенты, суммирование ведется по kv , v= 1,. . ., т, от 0 до nv), так что, напр., подпространство многочленов степени 3 по каждому из тпеременных имеет размерность 4m. Иногда фиксируется суммарная степень многочлена n, тогда суммирование в (1) распространено на индексы, удовлетворяющие неравенству  Тригонометрический действительный полином порядка n1, . . ., п т по переменным t1, . . ., tm может быть записан в виде
Тригонометрический действительный полином порядка n1, . . ., п т по переменным t1, . . ., tm может быть записан в виде
 ,
,
где комплексные коэффициенты
 с индексами противоположного знака комплексно сопряжены, а суммирование ведется по kv, v=l, . . ., m, от -nv до nv. Этот полином можно также представить в виде линейной комбинации всевозможных произведений вида
с индексами противоположного знака комплексно сопряжены, а суммирование ведется по kv, v=l, . . ., m, от -nv до nv. Этот полином можно также представить в виде линейной комбинации всевозможных произведений вида  есть либо
есть либо  , либо
, либо 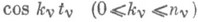 . Широкое применение находят многомерные сплайны, "склеенные" до определенной гладкости из "кусков" алгебраич. многочленов тпеременных. В случае т=2 наиболее простой вид имеют сплайны, склеенные из многочленов по прямым, параллельным осям координат. В качестве аппарата приближения применяются также функции g(t1 ,..., tm), являющиеся полиномами или сплайнами лишь по нек-рым из переменных. Для приближения непериодич. функций, заданных на всем пространстве
. Широкое применение находят многомерные сплайны, "склеенные" до определенной гладкости из "кусков" алгебраич. многочленов тпеременных. В случае т=2 наиболее простой вид имеют сплайны, склеенные из многочленов по прямым, параллельным осям координат. В качестве аппарата приближения применяются также функции g(t1 ,..., tm), являющиеся полиномами или сплайнами лишь по нек-рым из переменных. Для приближения непериодич. функций, заданных на всем пространстве  (или на неограниченном множестве из
(или на неограниченном множестве из 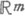 ), могут применяться целые функции экспоненциального типа, представимые в виде суммы абсолютно сходящегося степенного ряда
), могут применяться целые функции экспоненциального типа, представимые в виде суммы абсолютно сходящегося степенного ряда
 (2)
(2)
при условии, что для любого e>0 при всех комплексных t1, t2, ...,tm

где константа Me зависит только от e (см. [1]). Следует заметить, что в отличие от полиномов функция (2) определяется бесконечным числом параметров.
В многомерном случае справедлива теорема Вейерштрасса о возможности приблизить непрерывную на ограниченном замкнутом множестве
 функцию
функцию  или непрерывную на всем пространстве
или непрерывную на всем пространстве  с периодом 2p по каждому переменному функцию
с периодом 2p по каждому переменному функцию  алгебраическими (соответственно тригонометрическими) полиномами с любой наперед заданной степенью точности. Аналогичный факт имеет место и в пространствах Lp (Q).и (в периодич. случае)
алгебраическими (соответственно тригонометрическими) полиномами с любой наперед заданной степенью точности. Аналогичный факт имеет место и в пространствах Lp (Q).и (в периодич. случае)  . На линейные нормированные пространства функций тпеременных распространяются общие факты и теоремы о свойствах наилучшего приближения, о существовании, единственности и характеристич. свойствах функции наилучшего приближения, а также общие соотношения двойственности для приближения выпуклым множеством и, в частности, подпространством (см. [3], [4]). Однако получение конкретных реализаций этих теорем с учетом конкретной метрики и специфики приближающего подпространства в многомерном случае сопряжено с большими трудностями.
. На линейные нормированные пространства функций тпеременных распространяются общие факты и теоремы о свойствах наилучшего приближения, о существовании, единственности и характеристич. свойствах функции наилучшего приближения, а также общие соотношения двойственности для приближения выпуклым множеством и, в частности, подпространством (см. [3], [4]). Однако получение конкретных реализаций этих теорем с учетом конкретной метрики и специфики приближающего подпространства в многомерном случае сопряжено с большими трудностями.
Более полно исследованы вопросы связи порядка убывания наилучших приближений функций многих переменных алгебраическими и тригонометрич. полиномами, а также целыми функциями с гладкостными свойствами приближаемой функции.
Пусть Q - произвольное открытое множество в
 (в частности,
(в частности,  ), е - единичный вектор из
), е - единичный вектор из  , h>0 и Qhe- множество точек
, h>0 и Qhe- множество точек  таких, что отрезок
таких, что отрезок  . Если
. Если  , то величина
, то величина

наз. модулем непрерывности функция f(t1, . .., tm).в метрике Lp(Q).по направлению е. Величину
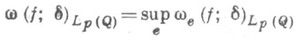
наз. модулем непрерывности функции f в Lp(Q).
В периодич. случае для наилучших приближений
 тригонометрич. полиномами
тригонометрич. полиномами
 функции
функции  , имеющей частные (вообще говоря, обобщенные по Соболеву) производные
, имеющей частные (вообще говоря, обобщенные по Соболеву) производные

(rv
 0 - целые,
0 - целые,  ), справедливы оценки
), справедливы оценки
 (3)
(3)
где ev - единичный вектор, направленный вдоль tv, аконстанта Мне зависит от f и nv. Для функции f из
 , имеющей обобщенные смешанные и несмешанные производные
, имеющей обобщенные смешанные и несмешанные производные

(r=(rl, . . ., r т)).порядка r=r1+. . .+r т, имеют место неравенства
 (4) Если
(4) Если

т. <е. если функции Drf удовлетворяют Гёлъдера условию, то
 (5)
(5)
В последнем случае обратная теорема утверждает, что если для функции
 при всех п=1,2, ... справедлива оценка (5), то существуют производные
при всех п=1,2, ... справедлива оценка (5), то существуют производные
 , удовлетворяющие при любом
, удовлетворяющие при любом  неравенствам
неравенствам
 (6) если 0<a<1, или
(6) если 0<a<1, или
 (7)
(7)
если a=1, где Кне зависит от длины |h|=(
 +...+
+...+ )1/2 вектора h=(h1 ,. . ., hm).
)1/2 вектора h=(h1 ,. . ., hm).
Теоремы, аналогичные приведенным, верны также для непериодич. функций
 , если в качестве аппарата приближения применяются целые функции экспоненциального типа. Приведенные результаты распространяются также на классы функций, гладкость к-рых описывается в терминах модулей непрерывности (модулей гладкости) более высокого порядка (см. [1]).
, если в качестве аппарата приближения применяются целые функции экспоненциального типа. Приведенные результаты распространяются также на классы функций, гладкость к-рых описывается в терминах модулей непрерывности (модулей гладкости) более высокого порядка (см. [1]).
В случае приближения функций
 алгебраич. многочленами
алгебраич. многочленами  на ограниченном параллелепипеде (и нек-рых других ограниченных множествах) доказаны прямые теоремы, аналогичные (3), (4) и (5). Обращение этих теорем, как и для функций, заданных на конечном отрезке, возможно лишь на множестве Q1, лежащем строго внутри Q. Известны обратные теоремы, предполагающие повышение порядка приближения вблизи границы множества Q(см. [13]), а также прямые теоремы, утверждающие возможность такого улучшения вблизи угловых точек (см. [14]). Необходимые и достаточные условия, обеспечивающие принадлежность функции f классу
на ограниченном параллелепипеде (и нек-рых других ограниченных множествах) доказаны прямые теоремы, аналогичные (3), (4) и (5). Обращение этих теорем, как и для функций, заданных на конечном отрезке, возможно лишь на множестве Q1, лежащем строго внутри Q. Известны обратные теоремы, предполагающие повышение порядка приближения вблизи границы множества Q(см. [13]), а также прямые теоремы, утверждающие возможность такого улучшения вблизи угловых точек (см. [14]). Необходимые и достаточные условия, обеспечивающие принадлежность функции f классу  (определяемому в метрике С(Q).условиями, аналогичными условиям (6), (7)) за счет повышения порядка приближения вблизи границы (как в одномерном случае), неизвестны (1983). Однако имеет место следующий результат отрицательного характера (см.[13]). Пусть
(определяемому в метрике С(Q).условиями, аналогичными условиям (6), (7)) за счет повышения порядка приближения вблизи границы (как в одномерном случае), неизвестны (1983). Однако имеет место следующий результат отрицательного характера (см.[13]). Пусть  . Не существует ни одной определенной на Qпоследовательности функций
. Не существует ни одной определенной на Qпоследовательности функций
 , обладающей следующими двумя свойствами:
, обладающей следующими двумя свойствами:
1) для всякой функции f из
 найдется постоянная Ми последовательность многочленов
найдется постоянная Ми последовательность многочленов

таких, что
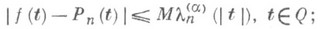 (8)
(8)
2) из того, что для определенной на Qфункции f существуют постоянная М>0 и последовательность многочленов Р п(t), удовлетворяющих неравенству (8), следует, что
 .
.
В качестве других примеров, отражающих специфику приближения функций многих переменных, можно привести следующие результаты.
Пусть
 - наилучшее приближение 2p-периодической функции f двух переменных тригонометрич. полиномами
- наилучшее приближение 2p-периодической функции f двух переменных тригонометрич. полиномами 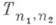 в метрике
в метрике  или
или 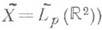 , а
, а  - наилучшее приближение f в
- наилучшее приближение f в  функциями
функциями  , являющимися тригонометрич. полиномами порядка п 1 по переменному t1 коэффициенты к-рых суть функции от t2. Аналогично определяются величины
, являющимися тригонометрич. полиномами порядка п 1 по переменному t1 коэффициенты к-рых суть функции от t2. Аналогично определяются величины  .
.
Если
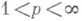 , то выполняются неравенства
, то выполняются неравенства

где А р зависит лишь от р.
Если же
 или
или  , то
, то
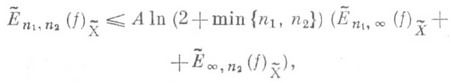 (9)
(9)
где А- абсолютная постоянная, и множитель In (2+min{n1, n2}) в неравенстве (9) нельзя заменить ни на какой другой, растущий при min{n1, n2}
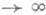 по порядку медленнее (см. [15]).
по порядку медленнее (см. [15]).
Принципиальные особенности возникают в задачах интерполирования функций многих переменных. Напр., существование алгебраического интерполяционного многочлена в отличие от одномерного случая существенно зависит от расположения узлов интерполяции. Разработаны, тем не менее, эффективные способы построения полиномов и сплайнов, интерполирующих функцию f(t1, . . ., tm).на определенным образом выбранной сетке узлов (см. Интерполирование), Для многомерных интерполяционных сплайнов в ряде случаев найдены порядковые оценки погрешности приближения как самой функции f, так и ее частных производных, более детально исследованы в этом направлении двумерные сплайны малого порядка, а также локальные (эрмитовы) сплайны любого порядка (см. [7], [10] - [12]). Среди других линейных методов приближения функций многих переменных сравнительно лучше исследованы кратные суммы Фурье и их различные средние. Здесь известны порядковые оценки приближения на классах функций, в нек-рых случаях найдена точная асимптотика (см. [5], [6], [8]). Лит.:[1] Никольский С. М., Приближение функций многих переменных и теоремы вложения, 2 изд., М., 1977; [2] Гутер Р. С., Кудрявцев Л. Д., Левитан Б. М., Элементы теории функций, М., 1963, с. 106-98; [3] Корнейчук Н. П., Экстремальные задачи теории-приближения, М., 1976; [4] Тихомиров В. М., Некоторые вопросы теории приближений, М., 1976; [5] Дзядык В. К., Введение в теорию равномерного приближения функций полиномами, М., 1977; [6] Тиман А. Ф., Теория приближения функций действительного переменного, М., 1960; [7] Стечкин С. Б., Субботин Ю. Н., Сплайны в вычислительной математике, М., 1976; [8] Степанец А. И., Равномерное приближение тригонометрическими полиномами. Линейные методы, К., 1981; (9] Лоран П. - Ж., Аппроксимация и оптимизация, пер. с франц., М., 1975; [10] Алберг Д да., Нильсон Э., Уолш Д ж., Теория сплайнов и ее приложения, пер. с англ., М., 1972; [11] Завьялов Ю. С., Квасов Б. И., Мирошниченко В. Л., Методы сплайн-функций, М., 1980; [12] Варга Р., Функциональный анализ и теория аппроксимации в численном анализе, пер. с англ., М., 1974; [13] Никольский С. М., "Сиб. матем. ж.", 1969, т. 10, № 5, с. 1075- 1083; [14] Брудный Ю. А., "Докл. АН СССР", 1970, т. 195, № 5, с. 1007-09; [15] Темляков В. Н., "Докл. АН СССР", 1975, т. 223, с. 1079-82. В. Н. Коновалов, Н. П. Корнейчук.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
