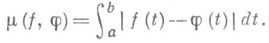ПРИБЛИЖЕНИЕ В СРЕДНЕМ

ПРИБЛИЖЕНИЕ В СРЕДНЕМ

приближение заданной и интегрируемой на промежутке [ а, b]функции f(t). функцией j(t), когда за меру погрешности принята величина


В более общем случае, когда


где s(t) - неубывающая на [ а, b]отличная от постоянной функция, говорят о сроднестепенном (с показателем q).приближении относительно распределения ds(t). Если s(t).абсолютно непрерывна и р(t)=s'(t), получают среднестепенное приближение с весом r(t), если же s(t) - ступенчатая функция со скачками ck в точках tk из [а, b], то приходят к взвешенному среднестепенному приближению в системе точек {tk} с мерой погрешности


Естественным образом эти понятия обобщаются на случай функций многих переменных.

Лит.:[1] Гончаров В. Л., Теория интерполирования и приближения функций, 2 изд., М., 1954; [2] Никольский С. М., Приближение функций многих переменных и теоремы вложения, 2 изд., М., 1977.

Н. П. Корнейчук, В. П. Моторный.


Математическая энциклопедия. — М.: Советская энциклопедия. . 1977—1985.

Игры ⚽ Поможем написать реферат

Смотреть что такое "ПРИБЛИЖЕНИЕ В СРЕДНЕМ" в других словарях:

  • НАИЛУЧШЕЕ ПРИБЛИЖЕНИЕ В СРЕДНЕМ — наилучшее приближение функции x(t)функциями u(t)из фиксированного множества F, когда мера (погрешность) приближения выражается с помощью интегральной метрики (см. Наилучшее приближение, Приближение в среднем). Н. П. Корнейчук, В. П. Моторный …   Математическая энциклопедия

  • ПРИБЛИЖЕНИЕ ФУНКЦИЙ — замена по определенному правилу функции f(t).близкой к ней в том или ином смысле функцией j(t). из заранее фиксированного множества (приближающего множества). Предполагается, что функция f определена на том множестве Qm мерного евклидова… …   Математическая энциклопедия

  • Теорема Тейлора — Экспоненциальная функция y = ex (сплошная красная линия) и соответствующий многочлен Тейлора четвёртого порядка (штрих пунктирная зелёная линия) вблизи начала координат …   Википедия

  • ЖИДКОСТЬ — агрегатное состояние в ва, промежуточное между твёрдым и газообразным. Ж. присущи нек рые черты твёрдого тела (сохраняет свой объём, образует поверхность, обладает определ. прочностью на разрыв) и газа (принимает форму сосуда, в к ром находится,… …   Физическая энциклопедия

  • Семейство слоновые —         Азиатский, или индийский, слон (Elephas maximus)*, на которого мы обыкновенно смотрим как на прообраз этого рода и семейства, есть большое, толстое, неуклюжее животное с массивной, широколобой головой, короткой шеей, сильным телом и… …   Жизнь животных

  • МЕДИЦИНСКОЕ ОБРАЗОВАНИЕ I — МЕДИЦИНСКОЕ ОБРАЗОВАНИЕ I. История медицинского образования. Первые достоверные сведения о М. о. относятся к древнейшим историческим памятникам восточной культуры. В Месопотамии кодекс Хаммураби (около 2250 г. до н. эры) уже занимается врачебными …   Большая медицинская энциклопедия

  • Приливы и отливы — (франц. marées, нем. Gezeiten, англ. tides) периодические колебания уровня воды вследствие притяжения Луны и Солнца. Общие сведения. П. всего заметнее по берегам океанов. Тотчас после малой воды наибольшего отлива, уровень океана начинает… …   Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

  • Климат Барнаула — Общая характеристика Тип климата Среднегодовая температура, °C Разность температур, °C резко континентальный 2,3 86,5 Температура Максимальная, °C Минимальная, °C 38,3 48,2 Осадки Количество осадков, мм Снежный покров, мес. 413 5 …   Википедия

  • Ломоносов, Михаил Васильевич — — ученый и писатель, действительный член Российской Академии Наук, профессор химии С. Петербургского университета; родился в дер. Денисовке, Архангельской губ., 8 ноября 1711 г., скончался в С. Петербурге 4 апреля 1765 года. В настоящее… …   Большая биографическая энциклопедия

  • Парадокс дней рождения — Парадокс дней рождения  это кажущееся парадоксальным утверждение, что вероятность совпадения дней рождения (числа и месяца) хотя бы у двух членов группы из 23 и более человек, превышает 50 %. С практической точки зрения это означает,… …   Википедия


Поделиться ссылкой на выделенное

Прямая ссылка:
… Нажмите правой клавишей мыши и выберите «Копировать ссылку»