- ПЕРЕХОДНЫЕ ВЕРОЯТНОСТИ
- вероятности перехода Маркова цепи
 . на отрезке времени [s, t]из состояния iв состояние j:
. на отрезке времени [s, t]из состояния iв состояние j:
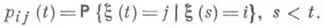
Ввиду основного свойства цепи Маркова для любых состояний
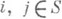 (где S - множество всех состояний цепи) и любых s<t<u
(где S - множество всех состояний цепи) и любых s<t<u
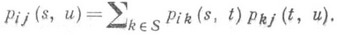
Обычно рассматриваются однородные цепи Маркова, для к-рых П. в. pij(s, t).зависят от длины отрезка [s, t], но не от его положения на оси времени:
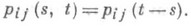
Для любых состояний i, j однородной цепи Маркова с дискретным временем последовательность pij(n).сходится по Чезаро, т. е. существует
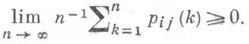
При нек-рых дополнительных условиях (а также для цепей с непрерывным временем) пределы существуют и в обычном смысле. См. Маркова цепь эргодическая, Маркова цепи положительный класс состояний.
П. в. pij(t).цепи Маркова с дискретным временем определяются значениями
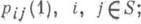 для любых
для любых
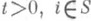
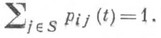
В случае цепей Маркова с непрерывным временем обычно предполагается, что П. в. удовлетворяют дополнительным условиям: все pij(t).измеримы как функции
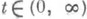 ,
,
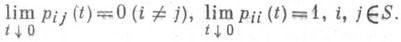
При этих предположениях существуют плотности вероятностей перехода
 (1)
(1)
если все
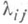 конечны и
конечны и  то П. в. pij(t)
то П. в. pij(t)
удовлетворяют системам дифференциальных уравнений Колмогорова - Чепмена
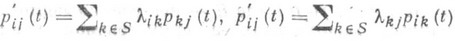 (2)
(2)
с начальными условиями
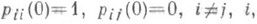
 (см. также Колмогорова уравнение, Колмогорова - Чепмена уравнение).
(см. также Колмогорова уравнение, Колмогорова - Чепмена уравнение).
При задании цепи Маркова плотностями перехода (1) ее П. в. pij(t).удовлетворяют условиям
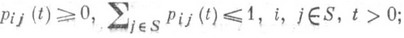
цепи, для к-рых
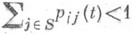 при нек-рых
при нек-рых 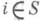 и t>0, наз. нерегулярными (тогда имеет место неединственность решения систем (2)); если
и t>0, наз. нерегулярными (тогда имеет место неединственность решения систем (2)); если 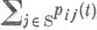 =1 для всех
=1 для всех  и t>0, то цепь наз. регулярной. Пример. Цепь Маркова x(t). с множеством состояний {0, 1, . . .} и плотностями перехода
и t>0, то цепь наз. регулярной. Пример. Цепь Маркова x(t). с множеством состояний {0, 1, . . .} и плотностями перехода
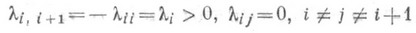
(т. н, процесс чистого размножения) нерегулярна тогда и только тогда, когда
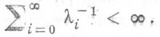
Пусть
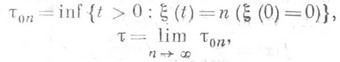
тогда
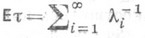
и при
 имеет место
имеет место 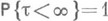 , т. е. траектория цепи x (t)."с вероятностью 1 за конечное время уходит в бесконечность" (см. также Ветвящихся процессов регулярность).
, т. е. траектория цепи x (t)."с вероятностью 1 за конечное время уходит в бесконечность" (см. также Ветвящихся процессов регулярность).
Лит.:[1]Чжун Кай-лай, Однородные цепи Маркова, пер. с англ., М., 1964. А. М. Зубков.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
