МАРКОВА ЦЕПЬ ЭРГОДИЧЕСКАЯ
- МАРКОВА ЦЕПЬ ЭРГОДИЧЕСКАЯ
однородная по времени цепь Маркова x(t), обладающая следующим свойством: существуют (не зависящие от i) величины

где
 - переходные вероятности. Распределение {р j} на множестве состояний цепи x(t) наз. стационарным распределением: если
- переходные вероятности. Распределение {р j} на множестве состояний цепи x(t) наз. стационарным распределением: если  при всех j, то
при всех j, то  при всех
при всех  и j. Вместе с основным свойством цепи Маркова
и j. Вместе с основным свойством цепи Маркова

это позволяет находить {р j},не вычисляя пределов в (1).
Пусть  - момент первого возвращения в состояние j (для цепи Маркова с дискретным временем), тогда
- момент первого возвращения в состояние j (для цепи Маркова с дискретным временем), тогда
 аналогичное (более сложное) соотношение имеет место для цепи Маркова с непрерывным временем.
аналогичное (более сложное) соотношение имеет место для цепи Маркова с непрерывным временем.
Траектории М. ц. э. удовлетворяют эргодич. теореме: если f(Х) - функция на множестве состояний цепи x(t)> т° в случае дискретного времени

в случае непрерывного времени первая сумма в левой части заменяется интегралом.
Цепь Маркова, для к-рой существуют такие  и
и 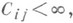 что при всех i, j, t
что при всех i, j, t

наз. геометрически эргод и ческой. Достаточным условием для геометрич. эргодичности М. ц. э. является условие Дёблина (см., напр., [1]), к-рое в рассматриваемом здесь случае дискретных (конечных или счетных) цепей Маркова может быть сформулировано так: существуют такие  и состояние j, что
и состояние j, что  Если выполнено условие Дёблина, то для констант в (2) справедливо соотношение
Если выполнено условие Дёблина, то для констант в (2) справедливо соотношение 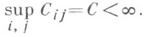
Необходимым и достаточным условием геометрич. эргодичности счетной цепи Маркова с дискретным временем является следующее (см. [3]): существуют такие числа f(j), q<1 и конечное множество Всостояний цепи, что

Лит.:[1] Дуб Д ж., Вероятностные процессы, пер. с англ., М., 195В; [2] Ч ж у н К а й - л а й, Однородные цепи Маркова, пер. с англ., М., 1964; [3] П о п о в Н. Н.,"Докл. АН СССР", 1977, т. 234, № 2, с. 316 - 19. А. М. Зубков.
Математическая энциклопедия. — М.: Советская энциклопедия.
И. М. Виноградов.
1977—1985.
Полезное
Смотреть что такое "МАРКОВА ЦЕПЬ ЭРГОДИЧЕСКАЯ" в других словарях:
МАРКОВА ЦЕПЬ — марковский процесс с конечным или счетным множеством состояний. Теория М. ц. возникла на основе исследований А. А. Маркова, к рый в 1907 положил начало изучению последовательностей зависимых испытаний и связанных с ними сумм случайных величин [1] … Математическая энциклопедия
Маркова цепь — Цепь Маркова последовательность случайных событий с конечным или счётным бесконечным числом исходов, характеризующаяся тем свойством, что, говоря нестрого, при фиксированном настоящем будущее независимо от прошлого. Названа в честь А. А. Маркова … Википедия
ЭРГОДИЧЕСКАЯ ТЕОРИЯ — Введение Э. т. (метрическая теория динамических систем) раздел теории динамических систем, изучающий их статистич. свойства. Возникновение Э. т. (1 я треть 20 в.) было стимулировано попытками доказать эргодическую гипотезу (термин введён П. и Т.… … Физическая энциклопедия
Цепь Маркова — Пример цепи с двумя состояниями Цепь Маркова последовательность случайных событий с конечным или счётным числом исходов, характеризующаяся тем свойством, что, го … Википедия
Цепь (матем.) — Цепь Маркова последовательность случайных событий с конечным или счётным бесконечным числом исходов, характеризующаяся тем свойством, что, говоря нестрого, при фиксированном настоящем будущее независимо от прошлого. Названа в честь А. А. Маркова … Википедия
Эргодическая цепь Маркова — Определение Пусть однородная цепь Маркова с дискретным временем и счётным числом состояний. Обозначим переходные вероятности за n шагов. Если существует дискретное распределение , такое что … Википедия
Цепи Маркова — Цепь Маркова последовательность случайных событий с конечным или счётным бесконечным числом исходов, характеризующаяся тем свойством, что, говоря нестрого, при фиксированном настоящем будущее независимо от прошлого. Названа в честь А. А. Маркова … Википедия
Неразложимая цепь Маркова — Определение Пусть однородная цепь Маркова с дискретным временем. Состояние j называется достижимым из состояния i, если существует n = n(i,j) такое, что . Пишут … Википедия
Периодическая цепь Маркова — Периодическое состояние это такое состояние цепи Маркова, которое навещается цепью только через промежутки времени, кратные фиксированному числу. Период состояния Пусть дана однородная цепь Маркова с дискретным временем с матрицей переходных… … Википедия
Возвратная цепь Маркова — Возвратное состояние это состояние Марковской цепи, посещаемое ею бесконечное число раз. Содержание 1 Определение 2 Критерий возвратности 3 Время возвращения … Википедия

 - переходные вероятности. Распределение {р j} на множестве состояний цепи x(t) наз. стационарным распределением: если
- переходные вероятности. Распределение {р j} на множестве состояний цепи x(t) наз. стационарным распределением: если  при всех j, то
при всех j, то  при всех
при всех  и j. Вместе с основным свойством цепи Маркова
и j. Вместе с основным свойством цепи Маркова 
 - момент первого возвращения в состояние j (для цепи Маркова с дискретным временем), тогда
- момент первого возвращения в состояние j (для цепи Маркова с дискретным временем), тогда  аналогичное (более сложное) соотношение имеет место для цепи Маркова с непрерывным временем.
аналогичное (более сложное) соотношение имеет место для цепи Маркова с непрерывным временем.
 и
и 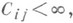 что при всех i, j, t
что при всех i, j, t
 и состояние j, что
и состояние j, что  Если выполнено условие Дёблина, то для констант в (2) справедливо соотношение
Если выполнено условие Дёблина, то для констант в (2) справедливо соотношение