ПЕРВЫЙ ИНТЕГРАЛ

обыкновенного дифференциального уравнения - отличная от постоянной и непрерывно дифференцируемая функция, производная к-рой вдоль решений данного уравнения тождественно равна нулю. Для скалярного уравнения

(*)

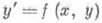П. и. есть функция F(x, у), находящаяся в левой части общего решения F(x, y)=C, где С - произвольная постоянная. Таким образом, F(x, у).удовлетворяет линейному уравнению

с частными производными 1-го порядка. П. и. может не существовать во всей области задания уравнения (*), однако в малой окрестности точки, в к-рой функция f(x, у).непрерывно дифференцируема, он всегда существует. П. и. определяется не единственным образом. Так, для уравнения П. и. является как функция x²+y², так, напр., и функция Знание П. и. нормальной системы

позволяет понизить порядок этой системы на единицу, а отыскание пфункционально независимых П. и. равносильно отысканию общего решения в неявном виде. Если - функционально независимые П. и., то всякий другой П. и. F(x, t).можно представить в виде

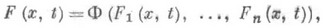
где Ф - нек-рая дифференцируемая функция.

Лит.:[1] Понтрягин Л. С., Обыкновенные дифференциальные уравнения, 4 изд., М., 1974. Н. Н. Ладис.