ПЕРЕВАЛА МЕТОД

ПЕРЕВАЛА МЕТОД

- метод вычисления асимптотики интегралов вида

(*)

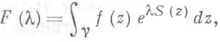где 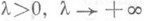- большой параметр, у - контур в комплексной плоскости z, функции f(z).и S(z) голоморфны в области D, содержащей у. Нули функции S'(z) наз. точками перевала функции S(z); точка перевала - седловая точка поверхности U== Re S(x+y). Суть П. м. состоит в следующем. Контур g деформируется в контур 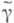с теми же концами, лежащий в Dи такой, что 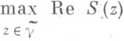достигается только в точках перевала или на концах 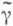(перевальный контур). Асимптотика интеграла (*) по перевальному контуру вычисляется с помощью Лапласа метода и равна сумме вкладов от указанных точек максимума. Вклад от точки z0 - это интеграл вида (*), взятый по малой дуге контура 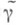, содержащей точку z0. Если z0 - внутренняя точка контура 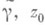- точка перевала и , то


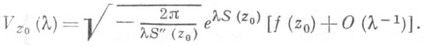
Перевальный контур обладает минимаксным свойством: на нем достигается


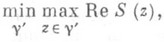
где минимум берется по всем контурам 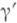, лежащим в Dи имеющим те же концы, что и g. Основная трудность при применении П. м.- отбор точек перевала, т. е. выбор перевального контура 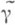, отвечающего g.

П. м. восходит к П. Дебаю [1]; идеи этого метода были высказаны ранее Б. Риманом (см. [2]). Вычисление вкладов от точек перевала и от концов контура см. в [3] - [9].

П. м.- по существу единственный метод, позволяющий вычислять асимптотику интегралов вида (*). С его помощью вычислены асимптотики преобразований Лапласа, Фурье, Меллина, экспоненты от полинома, многих специальных функций.

Пусть - ограниченное многообразие с краем размерности пи класса 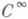, функции f(z), S(z).голоморфны в нек-рой области D, содержащей g, и dz=. Пусть достигается только в одной точке z0, к-рая 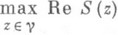является внутренней точкой g и невырожденной точкой перевала функции S(z), т. е. . Тогда вклад от z0 равен


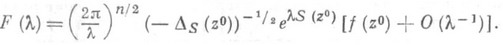
Лит.:[1] Dеbуе P., "Math. Ann.", 1909, Bd 67, S. 535-58; [2] Риман Б., Сочинения, пер. с нем., М.- Л., 1948; [3] Эрдейи А., Асимптотические разложения, пер. с англ., М., 1962; [4] Брейн Н. Г., Асимптотические методы в анализе, пер. с англ., М., 1961; [5] Евграфов М. А., Асимптотические оценки и целые функции, 2 изд., М., 1962; [6] Копсон Э.-Т., Асимптотические разложения, пер. с англ., М., 1966; [7] Оlvеr F. W. J., Asymptotics and special functions, N. Y. - [a. o.], 1974; [8] Риекстыньш Э. Я., Асимптотические разложения интегралов, т. 1-2, Рига, 1974-77; [9] Федорюк М. В., Метод перевала, М., 1977. М. В. Федорюк.


Математическая энциклопедия. — М.: Советская энциклопедия. . 1977—1985.

Игры ⚽ Поможем написать реферат

Полезное


Смотреть что такое "ПЕРЕВАЛА МЕТОД" в других словарях:

  • ПЕРЕВАЛА МЕТОД — способ оценкиинтегралов, подынтегральные ф ции к рых имеют резкий максимум. Обычно П …   Физическая энциклопедия

  • Перевала метод —         метод нахождения асимптотических выражений (См. Асимптотическое выражение) некоторых интегралов. Многие специальные функции (например, Цилиндрические функции, Сферические функции и др.) выражаются интегралами вида                  где f… …   Большая советская энциклопедия

  • Метод перевала — метод, использующийся для аппроксимации интегралов вида где это некоторые мероморфные функции, это некоторое большое число, а контур может быть бесконечным. Этот метод часто называется обобщением метода Лапласа. Содержание …   Википедия

  • Метод стационарной фазы — Метод стационарной фазы  метод, использующийся для аппроксимации интегралов вида: Содержание 1 Основы 2 Пример 3 Книги …   Википедия

  • Метод Лапласа — метод, использующийся для аппроксимации интегралов вида где это некоторая дважды дифференцируемая функция, это некоторое большое число. Идея метода Лапласа Предполагается, что функция имеет единственный глобальный ма …   Википедия

  • метод быстрейшего спуска или метод перевала — — [http://slovarionline.ru/anglo russkiy slovar neftegazovoy promyishlennosti/] Тематики нефтегазовая промышленность EN method of steepest desent …   Справочник технического переводчика

  • ЛАПЛАСА МЕТОД — асимптотических оценок метод вычисления асимптотики при l>0, интегралов Лапласа где W=[a, b] конечный отрезок, S действительная, f комплексная функции, достаточно гладкие при Асимптотика F(l) равна сумме вкладов от точек, в к рых достигается… …   Математическая энциклопедия

  • ДАРВИНА - ФАУЛЕРА МЕТОД — метод вывода канонического и большого канонич. распределений из микроканонического (см. Гиббса распределение). Для этого рассматривается ансамбль одинаковых статистич. систем, образующий в целом замкнутую систему, и характеризующая его функция… …   Математическая энциклопедия

  • СТАЦИОНАРНОЙ ФАЗЫ МЕТОД — метод вычисления асимптотики интегралов от быстро осциллирующих функций: где большой параметр, ограниченная область, функция S(x) (фаза) действительная, функция f(х) комплексная, и Если т. е. f финитна, и фаза S(x)не имеет стационарных точек (т.… …   Математическая энциклопедия

  • ДАРВИНА - ФАУЛЕРА МЕТОД — в статистической физике метод вычисления средних для большого числа N невзаимодействующих систем при фиксиров. полной энергии E при . Метод разработан Ч. Дарвином (Ch. Darwin) и P. Фаулером (R. Fowler) в 1922. Д. Ф. м. состоит в построении для… …   Физическая энциклопедия


Поделиться ссылкой на выделенное

Прямая ссылка:
… Нажмите правой клавишей мыши и выберите «Копировать ссылку»