ОБРЫВА ЦЕПЕЙ УСЛОВИЕ

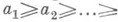
- условие конечности возрастающих или убывающих цепей в частично упорядоченном множестве. Условие обрыва убывающих цепей: для всякой цепи элементов частично упорядоченного множества Р найдется такой номер и, что Выполнение этого условия эквивалентно каждому из следующих свойств частично упорядоченного множества Р:

1) всякое непустое подмножество имеет хотя бы один минимальный (в М)элемент (условие минимальности);

2) все элементы из Робладают нек-рым свойством s, если этим свойством обладают все минимальные элементы множества Ри если справедливость свойства е для любого можно вывести из того, что е справедливо для всех 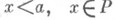(условие индуктивности).

Условие индуктивности позволяет для множеств с условием обрыва убывающих цепей проводить по индукции доказательства и построения. При этом если Рвполне упорядочено,- получается трансфинитная индукция, а если Ризоморфно множеству всех неотрицательных целых чисел,- обычная математич. индукция (см. Индукции аксиома).

Условие .обрыва возрастающих цепей (и эквивалентные ему утверждения) формулируется двойственным образом (см. Двойственности принцип в частично упорядоченных множествах). В решетке с условием обрыва возрастающих цепей каждый идеал - главный. Всякое конечное множество очевидно удовлетворяет обоим О. ц. у., однако обратное утверждение (конечность множества, удовлетворяющего этим двум условиям) неверно. Решетка с условиями обрыва убывающих и возрастающих цепей полна.

О. ц. у. используются в алгебре, в основном в применении к упорядоченному по включению множеству подсистем различных алгебраич. систем (см., напр., Артинов модуль, Артинова группа, Артиново кольцо, Композиционный ряд, Нётеров модуль, Нётерова группа, Нётерово кольцо).

Лит.:[1] Биркгоф Г., Теория структур, пер. с англ., М., 1952; [2] Курош А. Г., Лекции по общей алгебре, 2 изд., М., 1973; [3] Скорняков Л. А., Элементы теории структур, М., 1970.

Т. С. Фофанова.