ОБРАЩЕНИЕ ЭЛЛИПТИЧЕСКОГО ИНТЕГРАЛА

- проблема, состоящая в построении функции икак функции от zили однозначных сложных функций гида 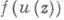в случае эллиптического интеграла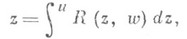

где R- рациональная функция от переменных z, w, связанных уравнением - многочлен 3-й или 4-й степени без кратных корней. Полное решение этой проблемы дали почти одновременно в 1827-29 Н. Абель (N. Abel) и К. Якоби (С. Jacobi), показав, что ее решение приводит к новым трансцендентным эллиптическим функциям.

Существенно иной подход к теории эллиптич. функций принадлежит К. Вейерштрассу (К. Weierstrass). Для эллиптич. интеграла I рода в нормальной форме Вейерштрасса

оказывается 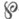-функцией Вейерштрасса с инвариантами (см. Вейерштрасса эллиптические функции). Для эллиптич. интеграла I рода в нормаль-ион форме Лежандра

обращение приводит к Якоби эллиптическим функциям.

Лит.:[1] Ахиезер Н. И., Элементы теории эллиптических функций, 2 изд., М., 1970; [2] Гурвиц А., Курант Р., Теория функций, пер. с нем., М., 1968.

Е. Д. Соломенцев.