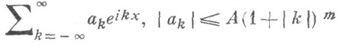ОБОБЩЕННОЙ ФУНКЦИИ ПРОИЗВОДНАЯ
- ОБОБЩЕННОЙ ФУНКЦИИ ПРОИЗВОДНАЯ
- слабое расширение операции обычного дифференцирования. Пусть обобщенная функция . Обобщенная (слабая) производная
. Обобщенная (слабая) производная
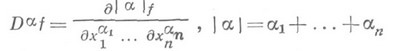
порядка  определяется равенством
определяется равенством
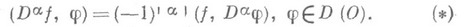
Так как операция  линейна и непрерывна из D(О)в D(О), то функционал
линейна и непрерывна из D(О)в D(О), то функционал  определяемый правой частью равенства (*), есть обобщенная функция из
определяемый правой частью равенства (*), есть обобщенная функция из  . Если
. Если  при всех
при всех  таких, что
таких, что 
Имеют место следующие свойства О. ф. п.: операция  линейна и непрерывна из D' (О)в D' (О);любая обобщенная функция из D' (О)бесконечно дифференцируема (в обобщенном смысле); дифференцирование He-зависит от порядка; справедлива формула Лейбница для дифференцирования произведения аf, где
линейна и непрерывна из D' (О)в D' (О);любая обобщенная функция из D' (О)бесконечно дифференцируема (в обобщенном смысле); дифференцирование He-зависит от порядка; справедлива формула Лейбница для дифференцирования произведения аf, где 
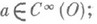
Пусть  Может случиться, что нек-рая обобщенная производная
Может случиться, что нек-рая обобщенная производная  может быть отождествлена с нек-рой
может быть отождествлена с нек-рой  (О)-функцией. В этом случае
(О)-функцией. В этом случае  - обобщенная производная типа функции.
- обобщенная производная типа функции.
Примеры. 1) где
где  - функция Хевисайда и d - функция Дирака.
- функция Хевисайда и d - функция Дирака.
2) Общее решение уравнения  в классе
в классе  есть произвольная постоянная.
есть произвольная постоянная.
3) Тригонометрический ряд
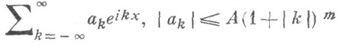
сходится в D' и его можно дифференцировать в D' почленно бесконечное число раз.
Лит.:[1] Schwartz L., Theorie des distributions, v. 1, P., 1950; [2] Соболев С. Л., Некоторые применения функционального анализа в математической физике, Новосиб., 1962,
В. С. Владимиров.
Математическая энциклопедия. — М.: Советская энциклопедия.
И. М. Виноградов.
1977—1985.
Полезное
Смотреть что такое "ОБОБЩЕННОЙ ФУНКЦИИ ПРОИЗВОДНАЯ" в других словарях:
Производная Пеано — ― одно из обобщений понятия производной. Пусть имеет место равенство где ― постоянные и при и . Тогда число называется обобщенной производной … Википедия
ОБОБЩЕННАЯ ПРОИЗВОДНАЯ — типа функции распространение понятия производной на некоторые классы недифференцируемых функций. Первое определение принадлежит С. Л. Соболеву (см. [1], [2]), к рый подошел к определению О. п. с точки зрения идеи введенного им понятия обобщенной… … Математическая энциклопедия
ЧАСТНАЯ ПРОИЗВОДНАЯ — первого порядка функции многих переменных производная функция по одной из переменных при условии, что все остальные переменные фиксированы. Напр., если функция f(x1, x2, ..., х п) определена в нек рой окрестности точки то Ч. и. функции f по… … Математическая энциклопедия
ПЕАНО ПРОИЗВОДНАЯ — одно из обобщений понятия производной. Пусть существует d>0 такое, что для всех tс |t|<d имеет место где постоянные и при Пусть . Тогда число нав. обобщенной производной Пеано порядка rфункции f в точке х 0. Обозначение: , в частности .… … Математическая энциклопедия
ОБОБЩЕННАЯ ФУНКЦИЯ — математическое понятие, обобщающее классич. понятие функции. Потребность в таком обобщении возникает во многих технич., физич. и математич. задачах. Понятие О. ф. дает возможность выразить в математически корректной форме такие идеализированные… … Математическая энциклопедия
ГОСТ 24346-80: Вибрация. Термины и определения — Терминология ГОСТ 24346 80: Вибрация. Термины и определения оригинал документа: 112. Автоколебания Колебания системы, возникающие в результате самовозбуждения Определения термина из разных документов: Автоколебания 137. Активная виброзащита… … Словарь-справочник терминов нормативно-технической документации
Прогноз — (Forecast) Определение прогноза, задачи и принципы прогнозирования Определение прогноза, задачи и принципы прогнозирования, методы прогнозирования Содержание Содержание Определение Основные понятия прогностики Задачи и принципы прогнозирования… … Энциклопедия инвестора
ГОСТ Р 52002-2003: Электротехника. Термины и определения основных понятий — Терминология ГОСТ Р 52002 2003: Электротехника. Термины и определения основных понятий оригинал документа: 128 (идеальный электрический) ключ Элемент электрической цепи, электрическое сопротивление которого принимает нулевое либо бесконечно… … Словарь-справочник терминов нормативно-технической документации
КРАЕВАЯ ЗАДАЧА — для эллиптического уравнения задача отыскания регулярного в области Dрешения иэллиптического уравнения удовлетворяющего нек рым дополнительным условиям на границе Г области D. Классические К. з. являются частными случаями следующей задачи: найти… … Математическая энциклопедия
ПОТЕНЦИАЛА ТЕОРИЯ — в первоначальном понимании учение о свойствах сил, действующих по закону всемирного тяготения. В формулировке этого закона, данной И. Ньютоном (I. Newton, 1687), речь идет только о силах взаимного притяжения, действующих на две материальные… … Математическая энциклопедия
 . Обобщенная (слабая) производная
. Обобщенная (слабая) производная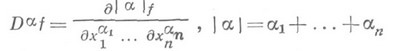
 определяется равенством
определяется равенством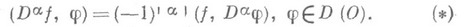
 линейна и непрерывна из D(О)в D(О), то функционал
линейна и непрерывна из D(О)в D(О), то функционал  определяемый правой частью равенства (*), есть обобщенная функция из
определяемый правой частью равенства (*), есть обобщенная функция из  . Если
. Если  при всех
при всех  таких, что
таких, что 
 линейна и непрерывна из D' (О)в D' (О);любая обобщенная функция из D' (О)бесконечно дифференцируема (в обобщенном смысле); дифференцирование He-зависит от порядка; справедлива формула Лейбница для дифференцирования произведения аf, где
линейна и непрерывна из D' (О)в D' (О);любая обобщенная функция из D' (О)бесконечно дифференцируема (в обобщенном смысле); дифференцирование He-зависит от порядка; справедлива формула Лейбница для дифференцирования произведения аf, где 
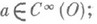
 Может случиться, что нек-рая обобщенная производная
Может случиться, что нек-рая обобщенная производная  может быть отождествлена с нек-рой
может быть отождествлена с нек-рой  (О)-функцией. В этом случае
(О)-функцией. В этом случае  - обобщенная производная типа функции.
- обобщенная производная типа функции. где
где  - функция Хевисайда и d - функция Дирака.
- функция Хевисайда и d - функция Дирака. в классе
в классе  есть произвольная постоянная.
есть произвольная постоянная.