Пеано — Пеано, Джузеппе Джузеппе Пеано Джузеппе Пеано (Giuseppe Peano; 1858 1932) итальянский математик. Внёс вклад в математическую логику, аксиоматику, философию математики. Создатель вспомогательного искусственного языка латино сине флексионе. Более… … Википедия
Пеано Д. — Джузеппе Пеано Джузеппе Пеано (Giuseppe Peano; 1858 1932) итальянский математик. Внёс вклад в математическую логику, аксиоматику, философию математики. Создатель вспомогательного искусственного языка латино сине флексионе. Более всего известен… … Википедия
Пеано Джузеппе — Джузеппе Пеано Джузеппе Пеано (Giuseppe Peano; 1858 1932) итальянский математик. Внёс вклад в математическую логику, аксиоматику, философию математики. Создатель вспомогательного искусственного языка латино сине флексионе. Более всего известен… … Википедия
Пеано, Джузеппе — Джузеппе Пеано Джузеппе Пеано (Giuseppe Peano; 1858 1932) итальянский математик. Внёс вклад в математическую логику, аксиоматику, философию мат … Википедия
Производная (обобщения) — У этого термина существуют и другие значения, см. Производная. В математике существует много различных обобщений понятия производной, так как она является базовой конструкцией дифференциального исчисления. Содержание 1 Односторонние производные … Википедия
Производная (обобщение) — В математике существует много различных обобщений понятия производной, так как она является базовой конструкцией дифференциального исчисления. Содержание 1 Односторонние производные 2 Анализ функций нескольких переменных … Википедия
Производная Пеано — ― одно из обобщений понятия производной. Пусть имеет место равенство где ― постоянные и при и . Тогда число называется обобщенной производной … Википедия
Джузеппе Пеано — (Giuseppe Peano; 1858 1932) итальянский математик. Внёс вклад в математическую логику, аксиоматику, философию математики. Создатель вспомогательного искусственного языка латино сине флексионе. Более всего известен как автор стандартной… … Википедия
Односторонняя производная — В математике существует много различных обобщений понятия производной, так как она является базовой конструкцией дифференциального исчисления. Содержание 1 Односторонние производные 2 Анализ функций нескольких переменных … Википедия
Дифференциал (математика) — У этого термина существуют и другие значения, см. Дифференциал (значения). Дифференциал (от лат. differentia разность, различие) линейная часть приращения функции. Содержание 1 Обозначения … Википедия
- постоянные и 
при 
Пусть 
. Тогда число 
нав. обобщенной производной Пеано порядка rфункции f в точке х 0. Обозначение: 
, в частности 
. Если существует f(r),(x0), то существует и 
. Если существует конечная обычная двусторонняя производная 
, то 
. Обратное неверно при r>1: для функции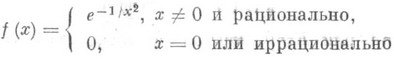 
,
, но не существует 
при 
(ибо f(x).разрывна при 
). Следовательно, не существует обычная производная 
при 
.
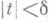имеет место 
- постоянные и 
при 
(
- число или символ 
). Тогда 
также наз. П. п. порядка rфункции f в точке x0. Введена Дж. Пеано (G. Реаnо). А. А. Конюшков.