ОБОБЩЕННАЯ ФУНКЦИЯ

- математическое понятие, обобщающее классич. понятие функции. Потребность в таком обобщении возникает во многих технич., физич. и математич. задачах. Понятие О. ф. дает возможность выразить в математически корректной форме такие идеализированные понятия, как плотность материальной точки, точечного заряда, точечного диполя, (пространственную) плотность простого или двойного слоя, интенсивность мгновенного источника и т. д. С другой стороны, в понятии О. ф. находит отражение тот факт, что реально нельзя измерить значение физич. величины в точке, а можно измерять лишь ее средние значения в достаточно малых окрестностях данной Toq-ки. Таким образом, техника О. ф. служит удобным и адекватным аппаратом для описания распределений различных физич. величин. Поэтому иначе О. ф. наз. распределениями (distributions).

О. ф. были введены впервые в кон. 20-х гг. 20 в. П. Дираком (P. Dirac, см. [1]) в его исследованиях по квантовой механике, где он систематически использует понятие б-функции и ее производных (см. Дельта-функция). Основы математич. теории О. ф. были заложены С. Л. Соболевым [2] в 1936 при решении задачи Коши для гиперболич. уравнений, а в 50-х гг. Л. Шварц (см. [3]) дал систематич. изложение теории О. ф. и указал многие применения. В дальнейшем теория О. ф. интенсивно развивалась многими математиками и физиками-теоретиками, главным образом в связи с потребностями теоретич. и математич. физики и теории дифференциальных уравнений (см. [4] - [7]). Теория О. ф. далеко продвинута, имеет многочисленные применения и широко вошла в обиход математика, физика и инженера.

Формально О. ф. f определяется как линейный непрерывный функционал над тем или иным векторным пространством достаточно "хороших" (основных) функций 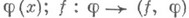. Важным примером основного пространства является пространство D(О)- совокупность финитных (О)-функций в открытом множестве , снабженная топологией строгого индуктивного предела (объединения) пространств 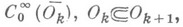Пространство есть совокупность -функций с носителем в , снабженная топологией счетного числа норм

Примером основной функции из служит "шапочка":

Сопряженное к D(О)пространство есть пространство О. ф. D' (О); Сходимость последовательности О. ф. из D' (О)определяется как слабая сходимость функционалов из , т. е. означает, что 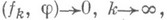для всех .

Для того чтобы линейный функционал f на D(О)был О. ф. в О, т. е., необходимо и достаточно, чтобы для любого открытого множества существовали числа Ки т такие, что

Если в неравенстве (1) целое число тможно выбрать независящим от О', то О. ф. f имеет конечный порядок; наименьшее такое тназ. порядком f в О. Таким образом, в силу (1), всякая О. ф. f из D' (О)имеет конечный порядок в любом

Пространство D' (О)- полное: если последовательность О. ф.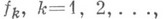из D' (О)такова, что для любой функции числовая последовательность сходится, то функционал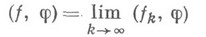

принадлежит D' (О).

Простейшими примерами О. ф. являются функционалы, порождаемые локально суммируемыми в Офункциями

О. ф., определяемые локально суммируемыми в Офункциями f(x)по формуле (2), наз. регулярными О. ф. в О;остальные О. ф. наз. сингулярными. Между локально суммируемыми в Офункциями и регулярными О. ф. в Осуществует взаимно однозначное соответствие. В этом смысле "обычные", т. е. локально суммируемые в О, функции являются (регулярными) О. ф. из D' (О).

Примером сингулярной О. ф. в 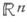служит d-функция Дирака

Она описывает плотность массы 1, сосредоточенной в точке х=0. При этом "шапочка" (слабо) аппроксимирует -функцию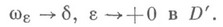

Пусть и - "шапочка". Тогда функция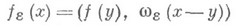

из наз. регуляризацией f, и в . Более того, всякая f из 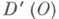есть слабый предел функций из D(O). Последнее свойство иногда берется в качестве исходного для определения О. ф., что вместе с теоремой о полноте пространства О. ф. приводит к эквивалентному определению О. ф. [8]. О. ф., вообще говоря, не имеют значений в отдельных точках. Тем не менее можно говорить о совпадении О. ф. с локально суммируемой функцией на открытом множестве: О. ф. f из D' (О)совпадает в с локально суммируемой в О' функцией 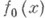, если ее сужение на О' есть f₀, т. е. в соответствии с (2)

для всех 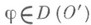, при этом считается

В частности, при получается определение того, что О. ф. fобращается в нуль в О'. Множество точек О, ни в какой окрестности к-рых О. ф. не обращается в нуль, наз. носителем О. ф. f и обозначается supp f. Если то О. ф. f наз. финитной в О.

Справедлива теорема окусочном склеивании обобщенной функции: пусть в окрестности каждой точкизадана О. ф. f_y из , причем элементы f_y согласованы, т. е.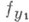 в тогда существует О. ф. f из D' (О), совпадающая с f_y в U_y при всех

Примеры обобщенных функций.

1) -функция Дирака:

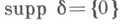
2) О. ф. 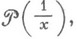определяемая равенством

наз. конечной частью, или главным значением, интеграла от функции ; сингулярна в , однако на открытом множестве она регулярна и совпадает с

3) Поверхностная -функция. Пусть S- кусочно гладкая поверхность и - непрерывная функция на S. О. ф. 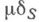определяется равенством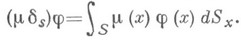

При этом 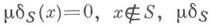- сингулярная О. ф.

Эта О. ф. описывает пространственную плотность масс или зарядов, сосредоточенных на поверхности Sс поверхностной плотностью m (плотность простого слоя).

Линейные операции над О. ф. вводятся как расширение соответствующих операций над основными функциями.

а) Замена переменных. Пусть 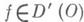и - неособенное линейное преобразование Она O₁ О. ф.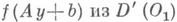 определяется равенством

Так как операция 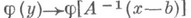- изоморфизм D(O)на D(O₁), то операция - изоморфизм D' (О)на D' (O₁). В частности, если 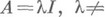,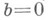(- подобие (с отражением при )),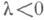

то

Формула (3) позволяет определить трансляционно инвариантные, сферически симметричные, центрально симметричные, однородные, периодические, лоренц-инвариантные и т. д. О. ф.

Пусть функция имеет только простые нули на оси . Функция 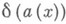определяется равенством

б) Произведение. Пусть 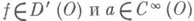Произведение определяется равенством

Оказывается, что 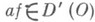и для обычных локально суммируемых функций произведение af совпадает с обычным умножением функций f(x) и a(x)

Однако эта операция произведения не допускает распространения на любые О. ф. так, чтобы она была ассоциативной и коммутативной. Действительно, в противном случае получилось бы противоречие:

В нек-рых классах О. ф. такое произведение можно определить, однако оно может оказаться неоднозначным.

в) Дифференцирование. Пусть Обобщенная (слабая) производная О. ф. f

порядка определяется равенством

Так как операция 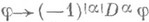линейна и непрерывна из D(О) в D (О), то функционал 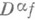, определяемый правой частью равенства (4), есть О. ф. из D' (О). Если

при всех а таких, что

Имеют место следующие свойства: операция 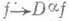линейна и непрерывна из D' (О)в D' (О), любая О. ф. из D' (О)бесконечно дифференцируема (в обобщенном смысле); дифференцирование не зависит от порядка; справедлива формула Лейбница для дифференцирования произведения аf, где ; дифференцирование не увеличивает носителя; всякая О. ф. f из D' (О)во всяком открытом множестве есть нек-рая производная от непрерывной функции в О';любое дифференциальное уравнение , с постоянными коэффициентами разрешимо в D' (О), если О- выпуклая область; любая О. ф. f порядка Nс носителем в точке 0 единственным образом представляется в виде

Примеры. 10) ,

где - функция Хевисайда (функция включения):

11)

описывает плотность зарядов, соответствующих диполю момента +1 в точке х=0 и ориентированного вдоль положительного направления оси х.

12) Обобщением является нормальная производная от плотности простого слоя на ориентируемой поверхности S: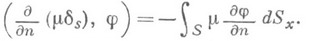

О. ф. описывает пространственную плотность зарядов, соответствующую распределению диполей на поверхности Sс поверхностной плотностью момента m, и ориентированных вдоль заданного направления нормали пна S(плотность двойного слоя).

13)Общее решение уравненияв классе есть , где С- произвольная постоянная.

14) Общее решение уравнения 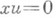в классе есть

15)

16) Тригонометрический ряд 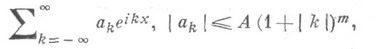сходится в 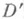и его можно дифференцировать в почленно бесконечное число раз.

г)Прямое произведение. Пусть 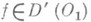и . Прямое произведение определяется по формуле

Так как операция линейна и непрерывна из в , то функционал , определяемый формулой (5), есть О. ф. из Прямое произведение - коммутативная и ассоциативная операция, причем

О. ф.из не зависит от переменной у, если она представима в виде в этом случае пишется

Примеры.

18)

19) Общее решение в уравнения колебаний однородной струны задается формулой

где 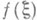и - произвольные О. ф. из

д) Свертка. Пусть О. ф. f и gиз 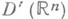обладают тем свойством, что их прямое произведение допускает расширение на функции вида , где пробегает , в следующем смысле: для всякой последовательности функций из со свойствами

(на любом компакте), числовая последовательность имеет предел, не зависящий от последовательности 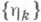. Этот предел наз. сверткой О. ф. f и gи обозначается , так что

Из полноты пространства следует, что Как показывают элементарные примеры, свертка существует не для любых пар f и g. Она заведомо существует, если одна из О. ф. финитна. Если свертка существует в 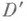, то она коммутативна и справедливы формулы дифференцирования свертки

Далее,

откуда из (7) получается

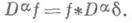
Наконец,

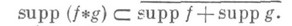
Как показывает пример:

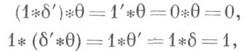
свертка - неассоциативная операция. Однако существуют ассоциативные (и коммутативные) сверточные алгебры. Единицей в них, в силу (8), служит -функция. Сверточную алгебру образует, напр., множество 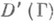, состоящее из О. ф. из с носителями в выпуклом остром и замкнутом конусе Г с вершиной в 0. Обозначение:

О. ф. 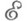из 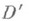наз. фундаментальным решением (функцией точечного источника) дифференциального оператора L(D)с постоянными коэффициентами, если она удовлетворяет уравнению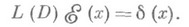

Зная фундаментальное решение оператора L(D), можно построить решение уравнения для тех fиз , для к-рых, свертка существует, и это решение дается формулой .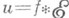

Примеры.

20) Ядро оператора дробного дифференцирования и дробного интегрирования

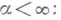
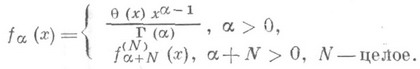
При этом -целое.

Если 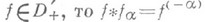есть первообразная порядка при > 0 (производная порядка -при <0).

е) Преобразование Фурье. Оно определяется для класса О. ф. 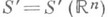медленного роста. Пространство основных функций состоит из -функций, убывающих на бесконечности вместе со всеми производными быстрее любой степени 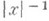. Топология в Sзадается счетным числом норм

При этом 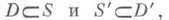где указанные вложения непрерывны. Локально суммируемые в функции медленного роста содержатся в , определяя по формуле (2) регулярные функционалы на S.

Всякая О. ф. из есть нек-рая производная от непрерывной функции медленного роста и, стало быть, имеет конечный порядок в

Преобразование Фурье О. ф. из S' определяется равенством

где

- классич. преобразование Фурье. Так как операция - изоморфизм S на S, то и операция - изоморфизм на 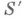, причем обратной операцией к Fслужит операция

Имеют место основные формулы для :

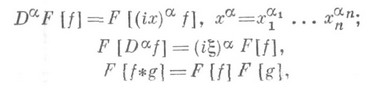
если gфинитна. Если О. ф. f - периодическая с п- периодом и ее можно разложить в тригонометрич. ряд

сходящийся к в ; здесь

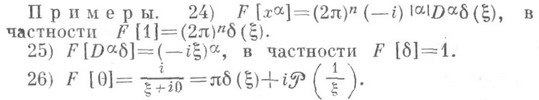
ж) Преобразование Лапласа. Пусть О. ф.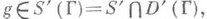где Г - замкнутый выпуклый острый конус. Пусть - сопряженный конус к Г. Преобразованием Лапласа О. ф. f наз. выражение

Операция 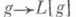осуществляет изоморфизм сверточной алгебры на алгебру Н(С), состоящую из функций f(z), голоморфных в трубчатой области 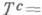. и удовлетворяющих условию роста: существуют числа 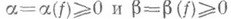такие, что для любого конуса существует число

такое, что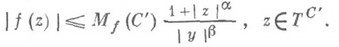

Обратное преобразование к преобразованию Лапласа Lзадается равенством

причем правая часть (10) не зависит от

Взаимно однозначное соответствие между и f(z), задаваемое равенствами (9) и (10), удобно изображать в виде следующей схемы: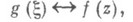

причем f наз. изображением g,a g- спектральной функцией функции f.

Всякая f(z) из алгебры Н(С). имеет граничное значиние при связанное со спектральной функцией gфункции f формулой 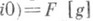согласно (9). Справедливы следующие основные формулы для преобразования Лапласа:

Лит.:[1] Дирак П. А. М., Основы квантовой механики, пер. с англ., 2 изд., М.- Л., 1937; [2] Соболев С. Л., "Матем. сб.", 1936, т. 1, с. 39-72; [3] SсhwartzL., Тheоrе des distributions, t. 1-2, P., 1950-51; [4] Боголюбов Н. Н., Логунов А. А., Тодоров И. Т., Основы аксиоматического подхода в квантовой теории поля, М., 1969; [5] Гельфанд И. М., Шилов Г. Е., Обобщенные функции, в. 1-3, М., 1958; [6]Владимиров В. С, Уравнения математической физики, 4 изд., М., 1981; [7] его ж е, Обобщенные функции в математической физике, 2 изд., М., 1979; [8] Антосик П., Минусинский Я., Сикорский Р., Теория обобщенных функций. Секвенциальный подход, пер. с англ., М., 1976.

В. С. Владимиров.