- НОРМАЛЬНЫЙ ОПЕРАТОР
- замкнутый линейный оператор А, определенный на плотном в гильбертовом пространстве H линейном многообразии DA, такой, что
 , где
, где  - оператор, сопряженный с А. Если А- Н. о., то
- оператор, сопряженный с А. Если А- Н. о., то  Обратно, выполнение этих условий обеспечивает нормальность А. Если А-Н. о., то:
Обратно, выполнение этих условий обеспечивает нормальность А. Если А-Н. о., то:  также нормален;
также нормален;  - Н. о. при любых
- Н. о. при любых  нормален в случае, когда этот оператор существует, если
нормален в случае, когда этот оператор существует, если 
 где В- ограниченный линейный оператор, то также
где В- ограниченный линейный оператор, то также 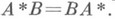
Для Н. о. Аимеют место:
1) мультипликативное разложение

где U- унитарный оператор, однозначно определяемый на ортогональном дополнении подпространства нулей операторов
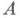 и
и  ;
;2) аддитивное разложение

где
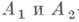 - однозначно определяемые самосопряженные операторы, перестановочные между собой.
- однозначно определяемые самосопряженные операторы, перестановочные между собой.Из аддитивного разложения следует, что для упорядоченной пары
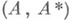 существует единственная двумерная спектральная функция
существует единственная двумерная спектральная функция 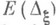 , где
, где 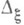 - двумерный интервал
- двумерный интервал 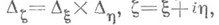 такая, что
такая, что 
Из этого разложения следует также, что Н. о. Аявляется функцией нек-рого самосопряженного оператора
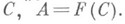 Обратно, всякая функция любого самосопряженного оператора есть Н. о.
Обратно, всякая функция любого самосопряженного оператора есть Н. о.Важным свойством Н. о. является равенство

 из к-рого следует, что спектральный радиус Н. о. Асовпадает с его нормой
из к-рого следует, что спектральный радиус Н. о. Асовпадает с его нормой  . Собственные элементы Н. о., соответствующие различным собственным значениям, ортогональны.
. Собственные элементы Н. о., соответствующие различным собственным значениям, ортогональны.Лит.:[1] Плеснер А. И., Спектральная теория линейных операторов, М., 1965; [2] Рудин У., Функциональный анализ, пер. с англ., М., 1975.
В. И. Соболев.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
