НЕРАЗРЕШИМОСТИ СТЕПЕНЬ

- класс эквивалентности 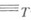, индуцированной отношением 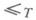тьюринговой сводимости на подмножествах натурального ряда (, если ). Иначе говоря, два множества принадлежат одной Н. с, если для каждого из них существует эффективная разрешающая процедура при возможности время от времени получать от "оракула" ответы на возникающие по ходу вычислений вопросы о принадлежности того или иного числа другому из рассматриваемых множеств (см. также Алгоритмическая сводимость). Н. с. определяют также как класс эквивалентности на множестве всюду определенных функций (отображающих натуральный ряд в себя), индуцированной отношением относительной рекурсивности (функция f рекурсивна относительно функции g, если для f существует рекурсивное определение, в к-ром в число исходных функций, помимо обычных, входит g);в этом случае Н. с. данной функции наз. также ее степенью невычислимости. Н. с. наз. также тьюринговыми степенями, или Т - степенями. Множество всех Н. с. при обоих подходах оказывается верхней полурешеткой (полуструктурой), причем получающиеся полурешетки Н. с. множеств и функций изоморфны, и в этом смысле приведенные определения эквивалентны.

Строение полурешетки Н. с. изучено довольно подробно (см. [1] - [3]). Элементарная теория полурешетки Н. с. неразрешима [6].

На множестве Н. с. определена операция скачка, сопоставляющая степени неразрешимости аН. с.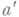, наибольшую среди Н. с, рекурсивно перечислимых относительно а(множество Врекурсивно перечисли мо относительно множества А, если Весть проекция рекурсивного относительно Амножества, а Н. с. bназ. рекурсивно перечислимой относительно Н. с. а, если bсодержит множество В, рекурсивно перечислимое относительно нек-рого А а). Операция скачка монотонна: из следует (но не обратно). Для всякой Н. с. существует такая Н. с. b, что Н. с. 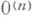являются наибольшими, достижимыми в классах 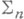и 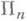арифметич. множеств.

Особый интерес представляют рекурсивно перечислимые Н. с. (Н. с. рекурсивно перечислимых множеств), образующие подполурешетку в полурешетке всех Н. с. Наибольшей среди рекурсивно перечислимых Н. с. является 0' (Н. с. полного множества). Вопрос о существовании рекурсивно перечислимых Н. с, отличных от 0 и 0' (т. н. проблема Поста), решен положительно (см. [4], [5]). При решении этой проблемы был развит приоритета метод. Полурешетка рекурсивно перечислимых Н. с. (в отличие от полурешетки всех Н. с.) плотна, причем в нее может быть вложено произвольное счетное частично упорядоченное множество. Для многих типов массовых проблем, возникающих в математике и состоящих в отыскании разрешающего алгоритма для некоторого множества (таких, как проблема тождества в теории групп, проблема разрешения конечно аксиоматизируемой элементарной теории и др.), доказано существование неразрешимых проблем соответствующего типа, имеющих произвольную рекурсивно перечислимую Н. с.

Исследовались Н. с. важнейших типов рекурсивно перечислимых множеств (так, все креативные множества имеют Н. с. 0', простые множества могут иметь любую ненулевую рекурсивно перечислимую И. с, максимальные - любую рекурсивно перечислимую Н. с. а, для к-рой а' = 0").

Понятие степени вводится и для других типов алго-ритмич. сводимости, отличных от тьюринговой (в частности, 1-, т-, tt- степени и др.), причем исследовался вопрос о распадении Н. с. на эти, "более мелкие", степени. Нек-рые из этих промежуточных типов сводимости оказываются связанными с оценкой сложности работы и задания алгоритмов (см. также Алгоритмическая теория информации).

Лит.:[1] Роджерс X., Теория рекурсивных функций и эффективная вычислимость, пер. с англ., М., 1972; [2] Шен Филд Д ж., Степени неразрешимости, пер. с англ., М., 1977; [3] Sасks G. E., Degrees of unsolvability, Princeton (N. Y.), 1963; [4] Mучник А. А., "Докл. АН СССР", 1956, т. 108, № 2, с. 194-97; [5] Friedbеrg R. M., "Proc. Nat. Acad. Sci. USA", 1957, v. 43, p. 236-38; [6] Lachlan A. H., "Z. math. Log. und Grundl. Math.", 1968, Bd 14, S. 457-72.

В. А. Душский.