Алгоритм Диффи

Алгори́тм Ди́ффи — Хе́ллмана (англ. Diffie-Hellman, DH) — алгоритм, позволяющий двум сторонам получить общий секретный ключ, используя незащищенный от прослушивания, но защищённый от подмены канал связи. Этот ключ может быть использован для шифрования дальнейшего обмена с помощью алгоритма симметричного шифрования.

Алгоритм был впервые опубликован Уитфилдом Диффи (Whitfield Diffie) и Мартином Хеллманом в 1976 году.

В 2002 году Хеллман предложил называть данный алгоритм «Диффи — Хеллмана — Меркля», признавая вклад Меркля в изобретение криптографии с открытым ключом.

Предисловие

До появление криптосистем с открытым ключом, приходилось пользоваться симметричными криптосистемами, что было не слишком удобно. В симметричных криптосистемах передача ключей между пользователями являлась сложной задачей, как правило приходилось использовать специального курьера . Диффи и Хеллман стали первыми, кто предложил использовать открытый ключ, тоесть обмен ключами между удаленными пользователями без применения защищенного канала. Эта схема стала называться протоколом обмена экспоненциальными ключами Диффи-Хеллмана

История

Схема обмена ключами Диффи — Хеллмана, изобретённая в 1976 году при сотрудничестве Уитфилда Диффи и Мартина Хеллмана, под сильным влиянием работы Ральфа Меркля (Ralph Merkle) о системе распространения публичных ключей, стала первым практическим методом для получения общего секретного ключа при общении через незащищенный канал связи. Для обеспечения устойчивости, по совету Джона Гилла (John Gill), была использована проблема дискретного логарифмирования.

Годом позже был изобретен первый алгоритм асимметричного шифрования RSA, который решил проблему общения через незащищённый канал кардинально.

В 2002 году Мартин Хеллман писал:

«Эта система … с тех пор известна под названием алгоритма Диффи — Хеллмана. Однако, когда система была впервые описана на бумаге Диффи и мной, это была система распространения публичных ключей, концепция которой была выработана Мерклем, и поэтому она должна называться „алгоритмом Диффи — Хеллмана — Меркля“, если её связывают с именами. Я надеюсь что это небольшое изменение поможет признанию равного вклада Меркля в изобретение криптографии с открытыми ключами.»^[1]

Патенты зарегистрированны в Соединенных штатах(истек 29 Апреля 1997) и Канаде. Группа Public Key Partners(PKPб Парнеры по открытым ключам), получила вместе с другими патентами в области криптографии с открытыми ключами получила лицензию на этот патент. В патенте U.S. Patent 4 200 770 (в настоящее время истекшем), описывающем данный алгоритм, изобретателями значатся Хеллман, Диффи и Меркль.

В декабре 1997 года была обнародована информация, что в 1974 году Малькольм Вильямсон изобрел математический алгоритм, основанный на коммутативности показателей при последовательном возведении в степень (то есть, $(b^x)^y = (b^y)^x = b^{xy}$), аналогичный алгоритму Диффи-Хеллмана.^[2]

Описание алгоритма

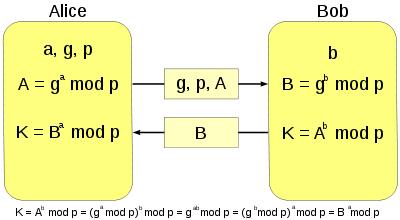
Предположим, что обоим абонентам известны некоторые два числа g и p (например, они могут быть «зашиты» в программное обеспечение), которые не являются секретными и могут быть известны также другим заинтересованным лицам. Для того, чтобы создать неизвестный более никому секретный ключ, оба абонента генерируют большие случайные числа: первый абонент — число a, второй абонент — число b. Затем первый абонент вычисляет значение $A=g^a \bmod p$ и пересылает его второму, а второй вычисляет $B=g^b \bmod p$ и передаёт первому. Предполагается, что злоумышленник может получить оба этих значения, но не модифицировать их (то есть у него нет возможности вмешаться в процесс передачи).

На втором этапе, первый абонент на основе имеющегося у него $a$ и полученного по сети $B$ вычисляет значение $B^a\bmod p=g^{ab}\bmod p$, а второй абонент на основе имеющегося у него $b$ и полученного по сети $A$ вычисляет значение $A^b\bmod p=g^{ab}\bmod p$. Как нетрудно видеть, у обоих абонентов получилось одно и то же число: $K=g^{ab}\bmod p$. Его они и могут использовать в качестве секретного ключа, поскольку здесь злоумышленник встретится с практически неразрешимой (за разумное время) проблемой вычисления $g^{ab} \bmod p$ по перехваченным $g^a \bmod p$ и $g^b \bmod p$, если числа $p, a, b$ выбраны достаточно большими.

Алгоритм Диффи — Хеллмана, где K — итоговый общий секретный ключ

При работе алгоритма, каждая сторона:

1. генерирует случайное натуральное число a — закрытый ключ
2. совместно с удалённой стороной устанавливает открытые параметры p и g (обычно значения p и g генерируются на одной стороне и передаются другой), где

   p является случайным простым числом

   g является первообразным корнем по модулю p

3. вычисляет открытый ключ A, используя преобразование над закрытым ключом

   A = g^a mod p

4. обменивается открытыми ключами с удалённой стороной
5. вычисляет общий секретный ключ K, используя открытый ключ удаленной стороны B и свой закрытый ключ a

   K = B^a mod p

   К получается равным с обеих сторон, потому что:

   B^a mod p = (g^b mod p)^a mod p = g^ab mod p = (g^a mod p)^b mod p = A^b mod p

В практических реализациях, для a и b используются числа порядка 10¹⁰⁰ и p порядка 10³⁰⁰. Число g не обязано быть большим и обычно имеет значение в пределах первого десятка.

Пример

Ева — криптоаналитик. Она читает пересылку Боба и Алисы, но не изменяет содержимого их сообщений.

• s = секретный ключ. s = 2
• g = открытое простое число. g = 5
• p = открытое простое число. p = 23
• a = секретный ключ Алисы. a = 6
• A = открытый ключ Алисы. A = g^a mod p = 8
• b = секретный ключ Боба. b = 15
• B = открытый ключ Боба. B = g^b mod p = 19

Алиса знает

p = 23

g = 5

a = 6

A = 56 mod 23 = 8

B = 5b mod 23 = 19

s = 196 mod 23 = 2

s = 8b mod 23 = 2

s = 196 mod 23 = 8b mod 23

s = 2

Алиса не знает

b=?

Боб знает

p = 23

g = 5

b = 15

B = 515 mod 23 = 19

A = 5a mod 23 = 8

s = 815 mod 23 = 2

s = 19a mod 23 = 2

s = 815 mod 23 = 19a mod 23

s = 2

Боб не знает

а=?

Ева знает

p = 23

g = 5

A = 5a mod 23 = 8

B = 5b mod 23 = 19

s = 19a mod 23

s = 8b mod 23

s = 19a mod 23 = 8b mod 23

Ева не знает

а=?

b=?

s=?

Diffie-Hellman с тремя и более участниками

Протокол обмена ключами можно расширить на случай с тремя и более участниками. В следующем примере Алиса, Боб и Кэрол вместе генерируют секретный ключ.

x = секретный ключ Алисы.

X = открытый ключ Алисы.

y = секретный ключ Боба.

Y = открытый ключ Боба.

z = секретный ключ Кэрол.

Z = открытый ключ Кэрол.

(1) Алиса выбирает случайное целое число x и вычисляет

X=$g^x$mod n

(2) Боб выбирает случайное целое число y и вычисляет

Y=$g^y$mod n

(3) Кэрол выбирает случайное целое число y и вычисляет

Z=$g^z$mod n

(4) Алиса посылает Бобу

$Z^'$=$Z^x$mod n

(5)Боб посылает Кэрол

$X^'$=$X^y$mod n

(6) Кэрол посылает Алисе

$Y^'$=$Y^z$mod n

(7) Алиса вычисляет

k=$Y^x$mod n

(8) Боб вычисляет

k=$Z^y$mod n

(9) Кэрол вычисляет

k=$X^z$mod n

Секретный ключ к=$g^{xyz}$mod n, никто из прослушивающих канал не могут узнать этот ключ. Протокол можно расширить на четырёх и более участником, просто добаляются новые участники и этапы вычисления.

Шифрование с открытым ключом

Данный алгоритм может также использоваться в качестве алгоритма шифрования с открытым ключом. В этом случае общая схема остаётся аналогичной приведённой выше, но с небольшими отличиями. Алиса не передаёт значения p, g и A Бобу напрямую, а публикует их заранее в качестве своего открытого ключа. Боб выполняет свою часть вычислений, после чего шифрует сообщение симметричным алгоритмом, используя K в качестве ключа, и передаёт шифротекст Алисе вместе со значением B. Однако такой подход не получил распространения, в этой области доминирует алгоритм RSA.

Обмен ключом без обмена ключем

Если имеется сообщество пользователей, каждый из пользователей может опубливать открытый ключ X=$g^x$mod n, в общей базе данных. Если Алиса хочет установить связь с Бобом, ей надо получить открытый ключ Боба и сгенерировать их общий секретный ключ. Алиса может зашифровать сообщение открытым ключом и послать его Бобу. Боб извлечет открытый ключ Алисы и найдет общий секретный ключ. Каждая пара пользователей может использовать свой уникальный секретный ключ, не требуя обмена данными между пользователями.Открытые ключи должны пройти сертификацию для защиты от нессанкционированного доступа, и эти ключи должны постоянно меняться.

Криптографическая стойкость

Криптографическая стойкость алгоритма Диффи — Хеллмана (то есть сложность вычисления K=g^ab mod p по известным p, g, A=g^a mod p и B=g^b mod p), основана на предполагаемой сложности проблемы дискретного логарифмирования. Однако хотя умение решать проблему дискретного логарифмирования позволит взломать алгоритм Диффи — Хеллмана, обратное утверждение до сих пор является открытым вопросом (другими словами, эквивалентность этих проблем не доказана).

Необходимо отметить, что алгоритм Диффи — Хеллмана работает только на линиях связи, надёжно защищённых от модификации. Если бы он был применим на любых открытых каналах, то давно снял бы проблему распространения ключей и, возможно, заменил собой всю асимметричную криптографию. Однако, в тех случаях, когда в канале возможна модификация данных, появляется возможность атаки «человек посередине». Атакующий заменяет сообщения переговоров о ключе на свои собственные и таким образом получает два ключа — свой для каждого из законных участников протокола. Далее он может перешифровывать переписку между участниками, своим ключом для каждого, и таким образом ознакомиться с их сообщениями, оставаясь незамеченным.

Задача Диффи-Хеллмана и задача дискретного логарифмирования

Стойкость разделенного ключа в протоколе Диффи-Хеллмана обеспечивается вычислением значенияе $g^{ab}mod p$ по заданным числам $g_a$ и $g_b$. Эта задача называется вычислительной проблемой Диффи-Хеллмана (CDH problem —Diffie-Hellman problem)

Вычислительная проблема Диффи-Хеллмана(в конечном поле)

ИСХОДНЫЕ ДАННЫЕ:
desq$F_q$ : описание конечного поля $F_q$ ;
g∈ $F_q^*$— порождающий элемент группы $F_q^*$ ;
$g_a$,$g_b$∈$F_q^*$, где 0 < a, b < q.
РЕЗУЛЬТАТ:
$g^{ab}$

Такая формулировка представляет собой общую постановку задачи в конечном поле $F_q$ представляет общий случай, для Диффи-Хеллмана используется специальный случай. Если бы проблему Диффи-Хеллмана было легко решить, то значение $g^{ab}$mod p можно было бы найти, зная числа p, g, $g^a$ и $g^b$, которые являются частью протокола. Предполагая, что противник обладает возможностями перехвата информации, следует предположить, что эти числа не являются для него секретом. Проблема Диффи-Хеллмана опирается на сложность вычисления дискретного логарифма (discrete logarithm problem)

Задача дискретного логарифмирования (в конечном поле)

ИСХОДНЫЕ ДАННЫЕ:
desq$F_q$ : описание конечного поля $F_q$ ;
g∈ $F_q^*$— порождающий элемент группы $F_q^*$ ;
h ∈${}_U$$F_q^*$
РЕЗУЛЬТАТ:
Уникальное число a < q, удовлетворяющее условию h = $g^a$.
Целое число a обозначается как $log_g$h.

Дискретное логарифмирование аналогично обычному логарифмированию, но в отличие от последнего имеет точное решение. Проблема Диффи-Хеллмана и задача дискретного логарифмирования считаются трудноразрешимыми.

Сформулируем точные предположения о неразрешимости проблемы Диффи-Хеллмана

Предположение. (Условия неразрешимости проблемы Диффи-Хеллмана) Алгоритмом решения проблемы Диффи-Хеллмана называется вероятностный полиномиальный алгоритм A с преимуществом ε > 0: ε = Prob[$g^{ab}$$\longleftarrow$A(desc($F_q$), g,$g^a$,$g^b$)]. Входные данные А указанны в определение (Вычислительная проблема Диффи-Хеллмана) (в конечном поле). Пусть IG — генератор вариантов, получающий на вход число $1^k$ время работы которого является полиномом от параметра k, а результатом — 1) desq($F_q$), где |q| = k, и 2) порождающий элемент g ∈$F_q^*$. Будем говорить, что генератор IG удовлетворяет условиям неразрешимости проблемы Диффи-Хеллмана, если для вариантов IG($1^k$) не существует алгоритма решения с преимуществом ε> 0, которое не является пренебрежимо малым по сравнению со всеми достаточно большими числами k.

См. также

• Zebedee

Примечания

1. ↑ Martin E. Hellman An overview of public key cryptography
2. ↑ M. J. Williamson. Non-secret encryption using a finite field. 21 января 1974.