МОНТЕЛЯ ТЕОРЕМА

- 1) М. т. о приближении аналитических функций многочленами: если D- открытое множество точек комплексной плоскости z, не содержащее точку , а - однозначная функция, аналитическая в каждой точке , то существует последовательность многочленов , сходящаяся к в каждой точке . Эта теорема является одной из основных в теории приближения функций комплексного переменного; получена П. Монтелем [1].

2) М. т. об условиях компактности семейства голоморфных функций (принцип компактности, см. [2]): пусть 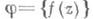- бесконечное семейство голоморфных функций в области Dкомплексной плоскости 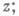тогда для того чтобы семейство 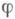было компактным, т. е. чтобы из любой последовательности можно было выделить подпоследовательность, равномерно сходящуюся внутри D, необходимо и достаточно, чтобы j было равномерно ограничено внутри D. Эта М. т. обобщается на области Dв пространстве (см. Компактности принцип).

3) М. т. об условиях нормальности семейства голоморфных функций (принцип нормальности, см. [2]): пусть 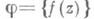- бесконечное семейство голоморфных функций в области Dкомплексной плоскости z. Если существуют два различных значения аи b, к-рые не принимаются ни одной функцией - нормальное семейство, т. е. из любой последовательности можно выделить подпоследовательность, равномерно сходящуюся внутри Dк голоморфной функции или к Условие этой М. т. можно несколько ослабить: достаточно потребовать, чтобы все функции 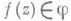не принимали одного из значений, напр, а, а другое значение Ъпринимали не более траз, Эта М. т. обобщается на случай областей Dв пространстве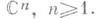

Лит.:[1] Montel P., Logons sur les series de polynomes a unevariable, P., 1910; [2] Mонтель П., Нормальные семейства аналитических функций, пер. с франц., М.- Л., 1936.

Е. Д. Соломенцев.