- МОНОИД
- термин, используемый для сокращения словосочетания "полугруппа с единицей". Таким образом, моноидом наз. множество М, на к-ром задана бинарная ассоциативная операция, обычно именуемая умножением, и в к-ром существует такой элемент е, что
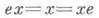 для любого
для любого  . Элемент еназ. единицей и часто обозначается 1. В любом М. имеется ровно одна единица. Если заданная в М. операция коммутативна, то ее часто наз. сложением, а единицу - нулем М. и обозначают 0.
. Элемент еназ. единицей и часто обозначается 1. В любом М. имеется ровно одна единица. Если заданная в М. операция коммутативна, то ее часто наз. сложением, а единицу - нулем М. и обозначают 0.Примеры М. 1) Множество всех отображений произвольного множества Sв себя является М. относительно операции последовательного выполнения (суперпозиции) отображений. Единицей служит тождественное отображение. 2) Множество эндоморфизмов любой универсальной алгебры Аявляется М. относительно операции суперпозиции, единица - тождественный эндоморфизм. 3) Всякая группа является М.
Всякую полугруппу Рбез единицы можно вложить в М. Для этого достаточно выбрать символ 1, не принадлежащий Р, и на множестве
 задать умножение следующим образом: 1*1 = 1, 1*x=х=x*1 для любого
задать умножение следующим образом: 1*1 = 1, 1*x=х=x*1 для любого  , на элементах из Роперация остается прежней. Всякий М. можно представить как М. всех эндоморфизмов нек-рой универсальной алгебры.
, на элементах из Роперация остается прежней. Всякий М. можно представить как М. всех эндоморфизмов нек-рой универсальной алгебры.Произвольный М. можно рассматривать также как категорию с одним объектом. Это позволяет сопоставить моноид Мдуальный (двойственный) моноиду
 Элементы обоих М. совпадают, а произведение хи ув
Элементы обоих М. совпадают, а произведение хи ув  полагается равным произведению ух в М.
полагается равным произведению ух в М.Развитие теории М. и сопряженных функторов выявило полезность определения М. в т. н. моноидальных категориях. Пусть в категории
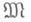 задан бифунктор
задан бифунктор  выделен объект Zи фиксированы естественные изоморфизмы
выделен объект Zи фиксированы естественные изоморфизмы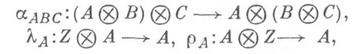
удовлетворяющие условиям когерентности. Объект Мназ. М. категории
 , если существуют такие мор-физмы
, если существуют такие мор-физмы  и
и  , что следующие диаграммы коммутативны:
, что следующие диаграммы коммутативны:
Если в качестве
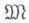 взять категорию множеств, в качестве
взять категорию множеств, в качестве  - декартово произведение, в качестве Z- любое одноточечное множество, а изоморфизмы
- декартово произведение, в качестве Z- любое одноточечное множество, а изоморфизмы  и
и 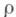 выбрать естественным образом
выбрать естественным образом 
 , то второе определение М.
, то второе определение М.оказывается равносильным исходному определению. Лит.:[1] Клиффорд А., Престон Г., Алгебраическая теория полугрупп, пер. с англ., т. 1-2, М., 1972; [2] Мас Lane S., Categories for the working mathematician, N. Y. [a. o.], 1971.
M. Ш. Цаленко.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
