- ПОЛИГОН
над моноидом R, R -полигон, операнд,- непустое множество с моноидом операторов. Точнее, непустое множество Аназ. левым П. над моноидом К, если для любых
и 
определено произведение 
, причем
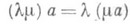
и
1а=а
для любых
. Правый П. определяется аналогично. Задание R-полигона Аравносильно заданию гомоморфизма j моноида R в моноид отображений множества Ав себя, переводящего 1 в тождественное отображение. При этом l а=b тогда и только тогда, когда
j(l)(а)=b.
В частности, каждое непустое множество можно рассматривать как П. над моноидом его отображений в себя. Таким образом, 11. тесно связан с представлением полугруппы преобразованиями.
Если А - универсальная алгебра, сигнатура к-рой W содержит лишь унарные операции, то Аможно превратить в П. над свободным моноидом Fс системой свободных образующих W, положив
для любых
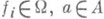. Если W - множество входных сигналов автомата с множеством состояний А, то Ааналогичным образом превращается в F-полигон (ср. Автоматов алгебраическая теория).
Отображение j R-полигона Ав R-полигон Вназ. гомоморфизмом, если
для любых 
и 
. При А-В получается определение эндоморфизма. Все эндоморфизмы полигона Аобразуют моноид, и Аможно рассматривать как П. над ним.
Эквивалентность 0 на Л-полигоне Аназ. конгруэнцией, если
влечет 
для любого 
. Множество классов конгруэнции q естественным образом превращается в R-полигон, называемый факторполигоном полигона Аи обозначаемый через A/q. Если А - полигон над R, то на Rможно определить отношение Ann A, положив 
, если la=ma для всех 
. Отношение Ann Аоказывается конгруэнцией моноида R, и Аестественным образом превращается в П. над фактормоноидом R/Ann А. Если полигон Авозник из нек-рого автомата, то описанный переход равносилен "склеиванию" одинаковым образом действующих последовательностей входных сигналов. Наряду с обычными для универсальных алгебр конструкциями прямого и подпрямого произведения, в теории П. рассматривается важная для алгебраич. теории автоматов конструкция сплетения. Свободное произведение (или копроизведение) П. совпадает с их дизъюнктным объединением.
На П. можно смотреть как на неаддитивный аналог модуля над кольцом, что служит богатым источником задач теории П. В частности, установлена связь П. с радикалами в полугруппах и исследуются связи свойств моноида со свойствами П. над ним. Напр., все левые R-полигоны проективны тогда и только тогда, когда R - одноэлементная группа, а инъективность всех П. над коммутативным моноидом Rравносильна наличию в Я нуля и порождаемости всех его идеалов идемпотентами (ср. Гомологическая классификация колец).
Если R- моноид с нулем 0, то можно говорить об R-полигоне Ас нулем как об R-полигоне с отмеченной точкой и, причем Оа=и для всех
. Теория П. с нулем имеет нек-рые особенности.
Каждый П. можно рассматривать как функтор из однообъектной категории в категорию множеств.
Лит.:[1] Алгебраическая теория автоматов, языков и полугрупп, пер. с англ., М., 1975; [2] Клиффорд А., Престон Г., Алгебраическая теория полугрупп, пер. с англ., т. 2, М., 1972: [3] Скорняков Л. А., в сб.: Модули, в. 3, Новосиб., 1973. с. 22-27; [4] Итоги науки и техники. Алгебра. Топология. Геометрия, т. 14, М., 1976, с. 57 -190.
Л. А. Скорняков.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
