МОНОИДАЛЬНОЕ ПРЕОБРАЗОВАНИЕ

раздутие, s-процесс,- специального вида бирациональный морфизм алгебраич. многообразий или биме-роморфный морфизм аналитич. ространств. Пусть, напр., X- алгебраич. многообразие (или произвольная схема), а - замкнутое подмногообразие, задаваемое пучком идеалов J. Моноидальным преобразованием Xс центром в Dназ.- проективный спектр градуированного пучка -алгебр 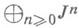. Если f: - структурный морфизм Х-схемы 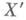, то пучок идеалов на (определяющий исключительную подсхему ) обратим. Это значит, что является дивизором в ; кроме того, f индуцирует изоморфизм между и X-D. М. п.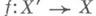схемы Xс центром в Dхарактеризуется следующим свойством универсальности [1]: пучок идеалов обратим и для любого морфизма , для к-рого 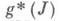обратим, существует единственный морфизм 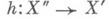такой, что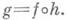

Аналогично определяется и характеризуется М. п. алгебраич. или аналитич. ространства Xс центром в замкнутом подпространстве .

Важный класс М. п. составляют допустимые моноидальные преобразования, к-рые выделяются тем условием, что центр Dтаких преобразований неособый, а X- нормально плоская схема вдоль D. Последнее означает, что все пучки являются плоскими модулями. Важность допустимых М. п. объясняется тем, что они не ухудшают особенности многообразия. Более того, доказано (см. [1]), что подходящая последовательность допустимых М. п. улучшает особенности, что позволило доказать теорему о разрешении особенностей алгебраич. многообразий над полем нулевой характеристики.

Особенно просто устроены допустимые М. п. неособых многообразий. Если М. п. с неособым центром , то снова неособое, а исключительное подмногообразие канонически изоморфно проективизации конормального пучка к Dв X. В частном случае, когда Dсостоит из одной точки, М. п. заключается в "раздутии" этой точки в целое проективное пространство касательных направлений. О поведении различных инвариантов ноособых многообразий (таких как кольцо Чжоу, когомологии, K-функтор, классы Чжэня) при допустимом М. п. см. [2] - [5].

Лит.:[1] Хиронака X., "Математика", 1965, т. 9, №6, с. 2-70; [2] Theorie des intersections et theoreme de Riemann-Roch, В.- Hdlh.- L., 1967; [3] Cohomologie l-adique et fonctions L(SGA-5), В.- Hdlb.- L., 1977; [4] Porteous I., "Proc. Cambridge Phil. Soc", 1960, v. 56, № 2, p. 118-24; [5] Mанин Ю. И., "Успехи матеы. наук", 1969, т. 24, в. 5, с. 3-86.

В. И. Данилов.